
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅⊆{x|x<4} | B. | $2\sqrt{3}∈\left\{{x|x<4}\right\}$ | C. | ∅∈{∅,{0},{1}} | D. | $\left\{{2\sqrt{3}}\right\}∈\left\{{x|x<4}\right\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:选择题
已知函数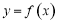 的定义域为
的定义域为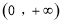 ,当
,当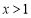 时,
时,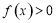 ,对任意的
,对任意的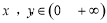 ,
,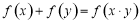 成立,若数列
成立,若数列 满足
满足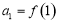 ,且
,且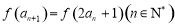 ,则
,则 的值为( )
的值为( )
A.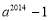 B.
B.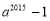 C.
C. D.
D.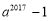
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:选择题
甲、乙、丙、丁四位同学各自在周六、周日两天中随机选一天郊游,则周六、周日都有同学参加郊游的情况共有( )
A.2种 B.10种 C.12种 D.14种
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com