
分析 (1)把已知等式变形,利用复数代数形式的乘除运算化简求得答案;
(2)直接利用求根公式求解;
(3)设出z=a+bi(a,b∈R),代入|z|-$\overline{z}$=$\frac{10}{1-2i}$,整理后可得关于a,b的方程组,求解方程组得答案;
(4)设出z=a+bi(a,b∈R),代入z2=7+24i,由复数相等的条件求得a,b的值得答案.
解答 解:(1)由$\overline{z}$i=i-1,得$\overline{z}=\frac{-1+i}{i}=\frac{(-1+i)(-i)}{-{i}^{2}}=1+i$,
∴$z=\overline{\overline{z}}=1-i$;
(2)由z2-z+2=0,得z=$\frac{1±\sqrt{7}i}{2}$;
(3)设z=a+bi(a,b∈R),则$|z|=\sqrt{{a}^{2}+{b}^{2}},\overline{z}=a-bi$,
代入|z|-$\overline{z}$=$\frac{10}{1-2i}$,得$\sqrt{{a}^{2}+{b}^{2}}-a+bi=\frac{10(1+2i)}{(1-2i)(1+2i)}$=2+4i,
∴$\left\{\begin{array}{l}{\sqrt{{a}^{2}+{b}^{2}}-a=2}\\{b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=3}\\{b=4}\end{array}\right.$,则z=3+4i;
(4)设z=a+bi(a,b∈R),则由z2=7+24i,
得a2-b2+2abi=7+24i,即$\left\{\begin{array}{l}{{a}^{2}-{b}^{2}=7}\\{2ab=24}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=4}\\{b=3}\end{array}\right.$或$\left\{\begin{array}{l}{a=-3}\\{b=-4}\end{array}\right.$,
∴z=4+3i或z=-4-3i.
点评 本题考查复数代数形式的混合运算,考查了复数相等的条件,训练了实系数一元二次方程的求法,是中档题.


科目:高中数学 来源: 题型:解答题
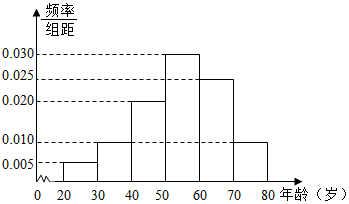 广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.
广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区跳广场舞的人的年龄进行了凋查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com