练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．已知实数x，y满足$\left\{{\begin{array}{l}{x-y-3≥0}\\{0＜x≤4}\end{array}}\right.$，则$\frac{y}{x}$的最大值是$\frac{1}{4}$．

    分析 先作出不等式组所表示的平面区域，由于$\frac{y}{x}$可以看做平面区域内的点与原点的连线的斜率，结合图形可求斜率最大值．

    解答 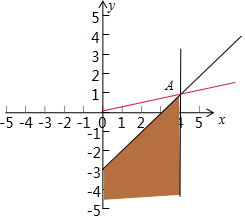解：作出不等式组所表示的平面区域如图所示，
    由于$\frac{y}{x}$可以看做平面区域内的点与原点的连线的斜率
    结合图形可知，当直线过A时，OA斜率最大，
    由于$\left\{\begin{array}{l}{x=4}\\{x-y-3=0}\end{array}\right.$可得A（4，1），此时k=$\frac{1}{4}$，
    故答案为：$\frac{1}{4}$．

    点评 本题主要考查了线性规划在求解最值中的应用，解题的关键是发现所求的式子的几何意义是平面区域内的点与原点的连线的斜率．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    4．如图，在边长为4的菱形ABCD中，∠BAD=60°，DE⊥AB于点E，将△ADE沿DE折起到△A1DE的位置，使A1E⊥EB．
    （1）求证：A1D⊥DC；
    （2）求直线ED与平面A1BC所成角的正弦值；
    （3）求二面角E-A1B-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

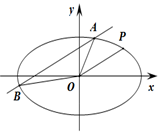    5．如图：已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$，与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点，且椭圆C过点P（2，1），若直线l与直线OP平行且与椭圆C相交于点A，B．
    （Ⅰ） 求椭圆C的标准方程；
    （Ⅱ） 求三角形OAB面积的最大值；
    （Ⅲ）求证：直线PA，PB与x轴围成一个等腰三角形．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．设集合M={x|x≥2}，N={x|x2-25＜0}，则M∩N=（　　）
    A．（1，5）B．[2，5）C．（-5，2]D．[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

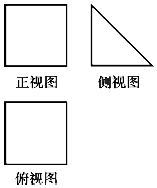    9．一块硬质材料的三视图如图所示，正视图和俯视图都是边长为10cm的正方形，将该木料切削、打磨，加工成球，则能得到的最大球的半径最接近（　　）
    A．3cmB．4cmC．5cmD．6cm

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．观察研究某种植物的生长速度与温度的关系，经过统计，得到生长速度（单位：毫米/月）与月平均气温的对比表如下：
    温度t（℃）-5068121520
    生长速度y24567810
    （1）求生长速度y关于温度t的线性回归方程；（斜率和截距均保留为三位有效数字）；
    （2）利用（1）中的线性回归方程，分析气温从-50C至200C时生长速度的变化情况，如果某月的平均气温是20C时，预测这月大约能生长多少．
    附：回归直线的斜率和截距的最小二乘法估计公式分别为：$\hat b=\frac{{\sum_{i=1}^n{（{{x_i}-\overline x}）（{{y_i}-\overline y}）}}}{{\sum_{i=1}^n{{{（{{x_i}-\overline x}）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline{xy}}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}，\hat a=\overline y-\hat b\overline x$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

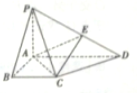    6．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD为直角梯形，BC∥AD，∠ABC=90°，且PA=AB=BC=$\frac{1}{2}$AD=1，点E在棱PD上（点E异于端点），且$\overrightarrow{PE}=λ\overrightarrow{PD}$．
    （1）当$λ=\frac{2}{3}$时，求异面直线PC与AE所成角的余弦值；
    （2）若二面角P-AC-E的余弦值为$\frac{\sqrt{3}}{3}$，求λ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已成椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右顶点分别为A1、A2，上下顶点分别为B2/B1，左右焦点分别为F1、F2，其中长轴长为4，且圆O：x2+y2=$\frac{12}{7}$为菱形A1B1A2B2的内切圆．
    （1）求椭圆C的方程；
    （2）点N（n，0）为x轴正半轴上一点，过点N作椭圆C的切线l，记右焦点F2在l上的射影为H，若△F1HN的面积不小于$\frac{3}{16}$n2，求n的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．设椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的一个顶点抛物线${x^2}=4\sqrt{3}y$的焦点重合，F1与F2分别是该椭圆的左右焦点，离心率$e=\frac{1}{2}$，且过椭圆右焦点F2的直线l与椭圆C交于M．N两点．
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）若$\overrightarrow{OM}•\overrightarrow{ON}=-2$，其中O为坐标原点，求直线l的方程；
    （Ⅲ）若AB椭圆C经过原点O的弦，且MN∥AB，判断$\frac{{{{|{AB}|}^2}}}{{|{MN}|}}$是否为定值？若是定值，请求出，若不是定值，说明理由．

    查看答案和解析>>

    同步练习册答案