
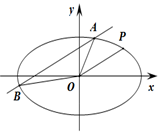
 如图:已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.
如图:已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.分析 (Ⅰ)由c=$\sqrt{6}$,a2=b2+c2=b2+6,将P(1,2)代入椭圆$\frac{{x}^{2}}{{b}^{2}+6}+\frac{{y}^{2}}{{b}^{2}}=1$,求得a和b,即可求得椭圆C的标准方程;
(Ⅱ)设直线l的方程为y=$\frac{1}{2}$x+m,代入椭圆方程,利用韦达定理,弦长公式,点到直线的距离公式,根据基本不等式的性质,即可求得三角形OAB面积的最大值;
(Ⅲ)设直线MA,MB的斜率分别为k1,k2,由已知条件推导出k1+k2=$\frac{{y}_{1}-1}{{x}_{1}-2}$•$\frac{{y}_{2}-1}{{x}_{2}-2}$=0,由此能证明直线PA,PB与x轴围成一个等腰三角形.
解答 解:(Ⅰ)双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点($\sqrt{6}$,0),即c=$\sqrt{6}$,
则a2=b2+c2=b2+6,将P(2,1)代入椭圆$\frac{{x}^{2}}{{b}^{2}+6}+\frac{{y}^{2}}{{b}^{2}}=1$,解得:b2=2,a2=8,
椭圆C的标准方程$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1$;
(Ⅱ) 由直线l平行于OP,设直线l的方程为y=$\frac{1}{2}$x+m,
由$\left\{\begin{array}{l}{y=\frac{1}{2}x+m}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1}\end{array}\right.$,得x2+2mx+2m2-4=0,
设A(x1,y1),B(x2,y2),则x1+x2=-2m,x1+x2=2m2-4,
由l与椭圆C有不同的两点,则△>0
△=4m2-4(2m2-4)>0,解得-2<m<2,且m≠0,
又|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{\sqrt{5}}{2}$•$\sqrt{4{m}^{2}-4(2{m}^{2}-4)}$=$\sqrt{5}$•$\sqrt{4-{m}^{2}}$,
点O到直线l的距离d=$\frac{丨2m丨}{\sqrt{5}}$,
∴△OAB的面积S=$\frac{1}{2}$•d•丨AB丨=|m|•$\sqrt{4-{m}^{2}}$=$\sqrt{{m}^{2}(4-{m}^{2})}$≤$\frac{{m}^{2}+4-{m}^{2}}{2}$=2,
当且仅当m2=4-m2,即m=±$\sqrt{2}$时取等号,
三角形OAB面积的最大值2;
(ⅡI)证明:设直线PA,PB的斜率分别为k1,k2,
则k1+k2=$\frac{{y}_{1}-1}{{x}_{1}-2}$•$\frac{{y}_{2}-1}{{x}_{2}-2}$=$\frac{(\frac{1}{2}{x}_{1}+m-1)({x}_{2}-2)+(\frac{1}{2}{x}_{2}+m-1)({x}_{1}-2)}{({x}_{1}-2)({x}_{2}-2)}$
=$\frac{{x}_{1}{x}_{2}+(m-2)({x}_{1}+{x}_{2})-4(m-1)}{({x}_{1}-2)({x}_{2}-2)}$=$\frac{2{m}^{2}-4+(m-2)(-2m)-4(m-1)}{({x}_{1}-2)({x}_{2}-2)}$=0,
∴直线PA,PB与x轴围成一个等腰三角形.
点评 本题考查椭圆方程的求法,考查求三角形面积的最大值和直线方程的求法,韦达定理及基本不等式的性质,解题时要认真审题,注意函数与方程思想的合理运用,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
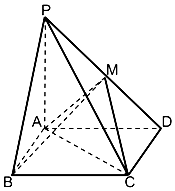 如图,在四棱锥P-ABCD,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.
如图,在四棱锥P-ABCD,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{{\sqrt{2}}}{2},1)$ | B. | $(0,\frac{{\sqrt{2}}}{2})$ | C. | $(\frac{{\sqrt{3}}}{2},1)$ | D. | $(0,\frac{{\sqrt{3}}}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{11π}{6}$ | B. | $\frac{11π}{6}$ | C. | $-\frac{7π}{6}$ | D. | $\frac{7π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
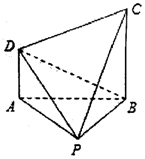 如图,在四棱锥P-ABCD中,CB⊥平面PAB,AD∥BC,且PA=PB=AB=BC=2AD=2.
如图,在四棱锥P-ABCD中,CB⊥平面PAB,AD∥BC,且PA=PB=AB=BC=2AD=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com