
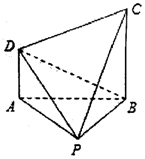
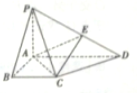
 如图,在四棱锥P-ABCD中,CB⊥平面PAB,AD∥BC,且PA=PB=AB=BC=2AD=2.
如图,在四棱锥P-ABCD中,CB⊥平面PAB,AD∥BC,且PA=PB=AB=BC=2AD=2.分析 (Ⅰ)分别取PC,PB的中点E,F,连结DE,EF,AF,证明AF⊥EF,AF⊥PB.推出AF⊥平面BPC,然后证明DE⊥平面BPC,即可证明平面DPC⊥平面BPC.….
(Ⅱ)解法1:连结BE,说明BE⊥CP,推出BE⊥平面DPC,过E作EM⊥PD,垂足为M,连结MB,说明∠BME为二面角C-PD-B的平面角.在△PDE中,求解即可.
解法2:以A为坐标原点,建立空间直角坐标系,求出相关点的坐标,求出平面PDC和面PBC的法向量,由空间向量的数量积求解二面角C-PD-B的余弦值即可.
解答  (本小题满分12分)
(本小题满分12分)
解:(Ⅰ)证明:如图,分别取PC,PB的中点E,F,
连结DE,EF,AF,由题意知,四边形ADEF为矩形,∴AF⊥EF.…(2分)
又∵△PAB为等边三角形,
∴AF⊥PB.又∵EF∩PB=F,
∴AF⊥平面BPC.…(4分)
又DE∥AF.
∴DE⊥平面BPC,又DE?平面DPC,
∴平面DPC⊥平面BPC.…(5分)
(Ⅱ)解法1:连结BE,则BE⊥CP,由(Ⅰ)知,
BE⊥平面DPC,过E作EM⊥PD,垂足为M,连结MB,则∠BME为二面角C-PD-B的平面角.…(7分)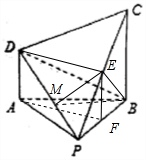
由题意知,DP=DC=$\sqrt{5}$,PC=$2\sqrt{2}$,∴$PE=\sqrt{2}$,∴$PD=\sqrt{3}$,
∴在△PDE中,$ME=\frac{DE•EP}{DP}=\frac{{\sqrt{30}}}{5}$.…(10分)
又$BE=\sqrt{2}$,
∴$BM=\frac{{4\sqrt{5}}}{5}$,∴$cos∠BME=\frac{ME}{BM}=\frac{{\sqrt{6}}}{4}$.…(12分)
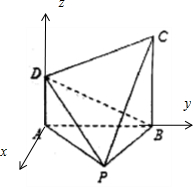
(Ⅱ)解法2:如图,以A为坐标原点,建立空间直角坐标系,则,A(0,0,0),B(0,2,0),$P(\sqrt{3},1,0)$,C(0,2,2),D(0,0,1).
$\overrightarrow{PB}=(-\sqrt{3},1,0)$,$\overrightarrow{PC}=(-\sqrt{3},1,2)$,$\overrightarrow{PD}=(-\sqrt{3},-1,1)$.…(8分)
设平面PDC和面PBC的法向量分别为$\overrightarrow n=(x,y,z)$,$\overrightarrow m=(a,b,c)$,
由$\left\{\begin{array}{l}\overrightarrow n•\overrightarrow{PD}=0\\ \overrightarrow n•\overrightarrow{PC}=0\end{array}\right.$,得$\left\{\begin{array}{l}x=-\sqrt{3}y\\ z=-2y\end{array}\right.$,令y=-1得$\overrightarrow n=(\sqrt{3},-1,2)$;
由$\left\{\begin{array}{l}\overrightarrow m•\overrightarrow{PD}=0\\ \overrightarrow m•\overrightarrow{PB}=0\end{array}\right.$,得$\left\{\begin{array}{l}b=\sqrt{3}a\\ c=2\sqrt{3}a\end{array}\right.$,令a=1得$\overrightarrow m=(1,\sqrt{3},2\sqrt{3})$.…(10分)
∴二面角C-PD-B的余弦值为$\frac{{\overrightarrow{m•}\overrightarrow n}}{{|{\overrightarrow m}|•|{\overrightarrow n}|}}=\frac{{\sqrt{3}-\sqrt{3}+4\sqrt{3}}}{{2\sqrt{2}×4}}=\frac{{\sqrt{6}}}{4}$.…(12分)
点评 本题考查平面与平面垂直的判定定理的应用,二面角的平面角的求法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:解答题
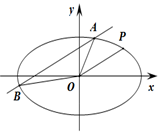 如图:已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.
如图:已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,与双曲线$\frac{x^2}{4}-\frac{y^2}{2}=1$有相同的焦点,且椭圆C过点P(2,1),若直线l与直线OP平行且与椭圆C相交于点A,B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,点E在棱PD上(点E异于端点),且$\overrightarrow{PE}=λ\overrightarrow{PD}$.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,BC∥AD,∠ABC=90°,且PA=AB=BC=$\frac{1}{2}$AD=1,点E在棱PD上(点E异于端点),且$\overrightarrow{PE}=λ\overrightarrow{PD}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
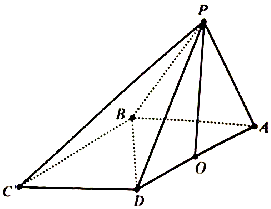 在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.
在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | -3 | C. | $\frac{1}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,矩形ABCD中,AB=2AD=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,构成四棱锥A1-BCDE,若M为线段A1C的中点,在翻转过程中有如下4个命题:
如图,矩形ABCD中,AB=2AD=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,构成四棱锥A1-BCDE,若M为线段A1C的中点,在翻转过程中有如下4个命题:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com