
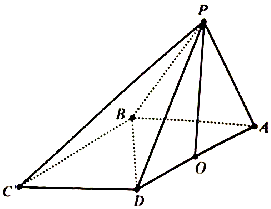
 在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.
在四棱锥P-ABCD中,$∠DBA=\frac{π}{2}$,$AB\underline{\underline∥}CD$,△PAB和△PBD都是边长为2的等边三角形,设P在底面ABCD的射影为O.分析 (1)证明PO⊥底面ABCD,说明点O为△ABD的外心,然后判断点O为AD中点.
(2)证明PO⊥面ABCD,推出BC⊥PO,证明CB⊥BO,BC⊥PO,证明CB⊥面PBO,推出BC⊥PB.
(3)以点O为原点,以OB,OD,OP所在射线为x轴,y轴,z轴建系,求出相关点的坐标,平面PAB的法向量,平面PBC的法向量,利用空间向量的数量积求解所以该二面角的余弦值即可.
解答 解:(1)证明:∵△PAB和△PBD都是等边三角形,
∴PA=PB=PD,
又∵PO⊥底面ABCD,
∴OA=OB=OD,
则点O为△ABD的外心,又因为△ABD是直角三角形,
∴点O为AD中点.
(2)证明:由(1)知,点P在底面的射影为点O,点O为AD中点,
于是PO⊥面ABCD,
∴BC⊥PO,
∵在Rt△ABD中,BD=BA,OB⊥AD,
∴$∠DBO=∠ODB=\frac{π}{4}$,
又$AB\underline{\underline∥}CD$,∴$∠CBD=\frac{π}{4}$,
从而$∠CBO=\frac{π}{2}$即CB⊥BO,
由BC⊥PO,CB⊥BO得CB⊥面PBO,
∴BC⊥PB.
(3)以点O为原点,以OB,OD,OP所在射线为x轴,y轴,z轴建系如图,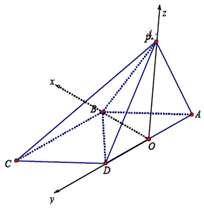
∵AB=2,则O(0,0,0),$A({0,-\sqrt{2},0})$,$B({\sqrt{2},O,O})$,$C({\sqrt{2},2\sqrt{2},0})$,$D({0,\sqrt{2},0})$,$P({0,0,\sqrt{2}})$,$\overrightarrow{BA}=({-\sqrt{2},-\sqrt{2},0})$,$\overrightarrow{BP}=({-\sqrt{2},0,\sqrt{2}})$,$\overrightarrow{BC}=({0,2\sqrt{2},0})$,
设面PAB的法向量为$\overrightarrow n=({x,y,z})$,则$\overrightarrow n•\overrightarrow{BA}=0$,$\overrightarrow n•\overrightarrow{BP}=0$,得$-\sqrt{2}x-\sqrt{2}y=0$,$-\sqrt{2}x+\sqrt{2}z=0$,
取x=1,得y=-1,z=1,
故$\overrightarrow n=({1,-1,1})$.
设面PBC的法向量为$\overrightarrow m=({r,s,t})$,则$\overrightarrow m•\overrightarrow{BC}=0$,$\overrightarrow m•\overrightarrow{BP}=0$,得s=0,$-\sqrt{2}r+\sqrt{2}t=0$,
取r=1,则t=1,故$\overrightarrow m=({1,0,1})$,
于是$cos<\overrightarrow m,\overrightarrow n>=\frac{\overrightarrow m•\overrightarrow n}{{|{\overrightarrow m}||{\overrightarrow n}|}}=\frac{{\sqrt{6}}}{3}$,
由图观察知A-PB-C为钝二面角,
所以该二面角的余弦值为$-\frac{{\sqrt{6}}}{3}$.
点评 本题考查直线与平面垂直的判定定理以及性质定理的应用,二面角的平面角的求法,考查空间想象能力以及逻辑推理能力计算能力.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $(\frac{{\sqrt{2}}}{2},1)$ | B. | $(0,\frac{{\sqrt{2}}}{2})$ | C. | $(\frac{{\sqrt{3}}}{2},1)$ | D. | $(0,\frac{{\sqrt{3}}}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3-2\sqrt{2}}{8}$ | B. | $\frac{2-\sqrt{2}}{4}$ | C. | $\frac{5-2\sqrt{2}}{8}$ | D. | $\frac{5-2\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
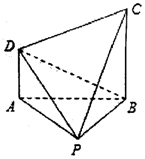 如图,在四棱锥P-ABCD中,CB⊥平面PAB,AD∥BC,且PA=PB=AB=BC=2AD=2.
如图,在四棱锥P-ABCD中,CB⊥平面PAB,AD∥BC,且PA=PB=AB=BC=2AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 工人在悬挂如图所示的一个正六边形装饰品时,需要固定六个位置上的螺丝,首先随意拧紧一个螺丝,接着拧紧距离它最远的第二个螺丝,再随意拧紧第三个螺丝,接着拧紧距离第三个螺丝最远的第四个螺丝,第五个和第六个以此类推,则不同的固定方式有48种.
工人在悬挂如图所示的一个正六边形装饰品时,需要固定六个位置上的螺丝,首先随意拧紧一个螺丝,接着拧紧距离它最远的第二个螺丝,再随意拧紧第三个螺丝,接着拧紧距离第三个螺丝最远的第四个螺丝,第五个和第六个以此类推,则不同的固定方式有48种.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com