
 ��ͼ������ABCD�У�AB=2AD=4��EΪ��AB���е㣬����ADE��ֱ��DE��ת�ɡ�A1DE����������A1-BCDE����MΪ�߶�A1C���е㣬�ڷ�ת������������4�����⣺
��ͼ������ABCD�У�AB=2AD=4��EΪ��AB���е㣬����ADE��ֱ��DE��ת�ɡ�A1DE����������A1-BCDE����MΪ�߶�A1C���е㣬�ڷ�ת������������4�����⣺| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
���� ��4������ֱ�����жϣ����ɵó����ۣ�
��� 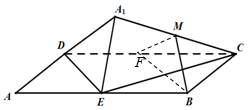 �⣺ȡCD�е�F������MF��BF����MF��DA1��BF��DE����ƽ��MBF��ƽ��A1DE����MB��ƽ��A1DE���ʢ���ȷ
�⣺ȡCD�е�F������MF��BF����MF��DA1��BF��DE����ƽ��MBF��ƽ��A1DE����MB��ƽ��A1DE���ʢ���ȷ
��A1C��ƽ��ABCD�е���ӰΪAC��AC��DE����ֱ��
�����ij��λ�ã�ʹDE��A1C����ȷ���ʢڲ���ȷ��
��CE��DE���ɵ�ƽ��A1DE��ƽ��ABCDʱ��A1D��CE���ʢ���ȷ��
��DE���е�O�Ƕ��㣬OA1=$\sqrt{2}$����A1������OΪԲ�ģ�$\sqrt{2}$Ϊ�뾶��Բ�ϣ��ʢ���ȷ��
��ѡ��C��
���� ���������������ж���Ӧ��Ϊ���壬���������桢����ƽ���봹ֱ���ж������ʶ������Ѷ��е���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
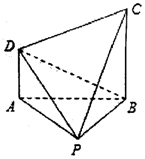 ��ͼ��������P-ABCD�У�CB��ƽ��PAB��AD��BC����PA=PB=AB=BC=2AD=2��
��ͼ��������P-ABCD�У�CB��ƽ��PAB��AD��BC����PA=PB=AB=BC=2AD=2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������P-ABCD �У���ABC=��BAD=90�㣬BC=2AD����PAB���PAD ���DZ߳�Ϊ2�ĵȱ������Σ�E ��BC���е㣮
��ͼ������P-ABCD �У���ABC=��BAD=90�㣬BC=2AD����PAB���PAD ���DZ߳�Ϊ2�ĵȱ������Σ�E ��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{6}$ | B�� | $\sqrt{3}$ | C�� | $\sqrt{2}$ | D�� | $\frac{\sqrt{6}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $��{-\frac{1}{2}��\frac{1}{3}}��$ | B�� | ��-1��2�� | C�� | $��{-\frac{4}{3}��-\frac{1}{2}}��$ | D�� | ��-2��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 10 | C�� | $4+3\sqrt{7}$ | D�� | $3+3\sqrt{17}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com