
分析 (1)求出原函数的导函数f′(x)=1-mex.当m≤0时,则f′(x)>0,函数f(x)为(-∞,+∞)上的增函数;当m>0时,由导函数的符号确定原函数的单调性;
(2)f(x)≤e2x?m≥$\frac{x}{{e}^{x}}-{e}^{x}$,设g(x)=$\frac{x}{{e}^{x}}-{e}^{x}$,利用导数求出g(x)的最大值,则实数m的取值范围可求;
(3)由f(x)有两个不同零点x1,x2,得${x}_{1}=m{e}^{{x}_{1}},{x}_{2}=m{e}^{{x}_{2}}$,两式作差可得${x}_{1}-{x}_{2}=m({e}^{{x}_{1}}-{e}^{{x}_{2}})$,即m=$\frac{{x}_{1}-{x}_{2}}{{e}^{{x}_{1}}-{e}^{{x}_{2}}}$.要证x1+x2>2,只要证明$m({e}^{{x}_{1}}+{e}^{{x}_{2}})$>2,即证$({x}_{1}-{x}_{2})\frac{{e}^{{x}_{1}}+{e}^{{x}_{2}}}{{e}^{{x}_{1}}-{e}^{{x}_{2}}}$>2.不妨设x1>x2,记t=x1-x2,则t>0,et>1,转化为(t-2)et+t+2>0.构造函数h(t)=(t-2)et+t+2(t>0),利用导数证明(t-2)et+t+2>0成立.
解答 (1)解:f′(x)=1-mex.
当m≤0时,f′(x)>0,函数f(x)为(-∞,+∞)上的增函数;
当m>0时,由f′(x)>0,得x<-lnm,∴f(x)在(-∞,-lnm)上为增函数;
由f′(x)<0,得x>-lnm,∴f(x)在(-lnm,+∞)上为减函数;
(2)解:f(x)≤e2x?m≥$\frac{x}{{e}^{x}}-{e}^{x}$,
设g(x)=$\frac{x}{{e}^{x}}-{e}^{x}$,则g′(x)=$\frac{1-{e}^{2x}-x}{{e}^{x}}$,
当x<0时,1-e2x>0,g′(x)>0,则g(x)在(-∞,0)上单调递增;
当x>0时,1-e2x<0,g′(x)<0,则g(x)在(0,-∞)上单调递减.
∴g(x)max=g(0)=-1,则m≥-1;
(3)证明:f(x)有两个不同零点x1,x2,则${x}_{1}=m{e}^{{x}_{1}},{x}_{2}=m{e}^{{x}_{2}}$,
因此${x}_{1}-{x}_{2}=m({e}^{{x}_{1}}-{e}^{{x}_{2}})$,即m=$\frac{{x}_{1}-{x}_{2}}{{e}^{{x}_{1}}-{e}^{{x}_{2}}}$.
要证x1+x2>2,只要证明$m({e}^{{x}_{1}}+{e}^{{x}_{2}})$>2,即证$({x}_{1}-{x}_{2})\frac{{e}^{{x}_{1}}+{e}^{{x}_{2}}}{{e}^{{x}_{1}}-{e}^{{x}_{2}}}$>2.
不妨设x1>x2,记t=x1-x2,则t>0,et>1,
因此只要证明$t•\frac{{e}^{t}+1}{{e}^{t}-1}$>2,即(t-2)et+t+2>0.
记h(t)=(t-2)et+t+2(t>0),h′(t)=(t-1)et+1,h″(t)=tet.
当t>0时,h″(t)=tet>0,∴h′(t)>h′(0)=0,
则h(t)在(0,+∞)上单调递增,∴h(t)>h(0)=0,
即(t-2)et+t+2>0成立.
∴x1+x2>2.
点评 本题考查导数知识的运用,考查函数的单调性与最值,考查导数的几何意义,考查恒成立问题,正确求导是关键,属难题.


科目:高中数学 来源: 题型:选择题
 如图,矩形ABCD中,AB=2AD=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,构成四棱锥A1-BCDE,若M为线段A1C的中点,在翻转过程中有如下4个命题:
如图,矩形ABCD中,AB=2AD=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,构成四棱锥A1-BCDE,若M为线段A1C的中点,在翻转过程中有如下4个命题:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x≤4} | B. | {x|x≥1} | C. | {x|1≤x≤4} | D. | {x|x≥-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
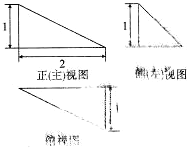 某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥的体积为( )
某三棱锥的三视图如图所示,其中三个视图都是直角三角形,则该三棱锥的体积为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如图,当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推.例如 6613 用算筹表示就是
中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如图,当表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位数用纵式表示,十位,千位,十万位用横式表示,以此类推.例如 6613 用算筹表示就是 ,则 8335 用算筹可表示为( )
,则 8335 用算筹可表示为( )| A. |  | B. | 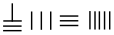 | C. |  | D. | 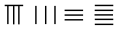 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com