
分析 由题意可知:顶点A,B为椭圆的两个焦点,利用正弦定理及椭圆的定义,求得a和b的关系,即可求得$\frac{5sinC}{sinA+sinB}$=3.
解答 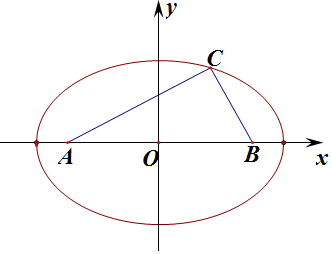 解:由椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1,长轴长2a=10,短轴长2b=8,焦距2c=6,
解:由椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1,长轴长2a=10,短轴长2b=8,焦距2c=6,
则顶点A,B为椭圆的两个焦点,
三角形ABC中,a=丨BC丨,b=丨AC丨,c=丨AB丨=6,a+b=丨BC丨+丨AC丨=10,
由正弦定理可知$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$=2R,
则sinA=$\frac{a}{2R}$,sinB=$\frac{b}{2R}$,sinC=$\frac{c}{2R}$,
$\frac{5sinC}{sinA+sinB}$=$\frac{5c}{a+b}$=$\frac{5×6}{10}$=3,
故答案为:3.
点评 本题考查椭圆的定义及正弦定理的应用,考查数形结合思想,考查计算能力,属于中档题.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | $4+3\sqrt{7}$ | D. | $3+3\sqrt{17}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $μ=\sqrt{3},Dξ=\sqrt{7}$ | B. | $μ=\sqrt{3},Dξ=7$ | C. | μ=3,Dξ=7 | D. | $μ=3,Dξ=\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某程序框图如图所示,其中$g(x)=\frac{1}{{{x^2}+x}}$,若输出的$S=\frac{2016}{2017}$,则判断框内应填入的条件为( )
某程序框图如图所示,其中$g(x)=\frac{1}{{{x^2}+x}}$,若输出的$S=\frac{2016}{2017}$,则判断框内应填入的条件为( )| A. | n<2017 | B. | n≤2017 | C. | n>2017 | D. | n≥2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,6] | B. | (-∞,-1) | C. | (6,+∞) | D. | (-∞,-1)∪(6,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com