Question

17．设函数f（x）=x²+2ax-b²+4（a、b∈R）
（1）若a∈{0，1，2}，b∈{-2，-1，0，1，2}，求函数f（x）有零点的概率．
（2）若a∈[-3，3]，b∈[0，3]，求函数g（x）=f（x）+5无零点的概率．

Answer 1

分析 （1）为古典概型，可得总的基本事件数为36，符合条件的由15个，可求概率；
（2）为几何概型，作图可得面积，作比值可得答案

解答 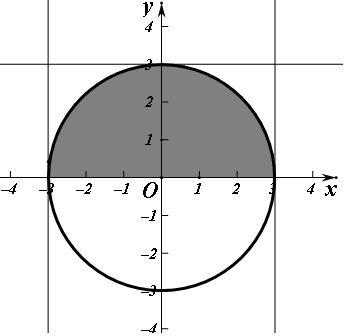解：（1）a∈{0，1，2}，b∈{-2，-1，0，1，2}，共有事件数为3×5=15；
设事件A为“函数f（x）=x²+2ax-b²+4有零点”，
即方程x²+2ax-b²+4=0有实根的条件为
△=4a²+4b²-16≥0，即a²+b²≥4，共有（0，-2），（0，2），（1，-2），（1，2），（2，-2），（2，2），（2，-1），（2，0），（2，1）共有9个事件，由古典概型的公式得到函数f（x）有零点的概率$\frac{9}{15}=\frac{3}{5}$．
（2）试验的全部结果所构成的区域为{（a，b）|-3≤a≤3，0≤b≤3} 
构成事件B=“函数g（x）=f（x）+5=x²+2ax-b²+9无零点”即△＜0的区域为
{（a，b）|a²+b²＜9  }即如图的阴影区域所示，由几何概型的公式得到所求概率为：$\frac{\frac{1}{2}π×{9}^{\;}}{6×3}=\frac{π}{4}$．

点评 本题考查古典概型和几何概型的求解，关键是明确概率模型性质，正确利用公式求值．