
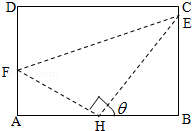
 如图,矩形ABCD的内接Rt△FHE,(H是直角顶点),H是AB的中点,E,F分别落在线段BC,AD上.已知AB=2,AD=$\sqrt{3}$,记∠BHE=θ.
如图,矩形ABCD的内接Rt△FHE,(H是直角顶点),H是AB的中点,E,F分别落在线段BC,AD上.已知AB=2,AD=$\sqrt{3}$,记∠BHE=θ.分析 (1)根据锐角三角函数的定义分别求出EH,FH,利用勾股定理求出EF,即可得出L关于θ的函数;
(2)令sinθ+cosθ=t,使用换元法求出L关于t的函数,根据θ的范围得出t的范围,从而得出L的最值.
解答 解:(1)在Rt△BEH中,∵BH=$\frac{1}{2}AB=1$,∠BHE=θ,
∴EH=$\frac{1}{cosθ}$,
在Rt△AFH中,AH=1,∠AHF=90°-θ,
∴FH=$\frac{1}{cos(90°-θ)}$=$\frac{1}{sinθ}$,
∵∠EHF=90°,
∴EF=$\sqrt{E{H}^{2}+F{H}^{2}}$=$\frac{1}{sinθcosθ}$.
∵$BE=tanθ≤\sqrt{3},AF=\frac{1}{tanθ}≤\sqrt{3}$,
∴$\frac{{\sqrt{3}}}{3}≤tanθ≤\sqrt{3}$,
∴$\frac{π}{6}≤$θ≤$\frac{π}{3}$.
∴L=$\frac{1}{cosθ}$+$\frac{1}{sinθ}$+$\frac{1}{sinθcosθ}$,θ∈[$\frac{π}{6}$,$\frac{π}{3}$].
(2)由(1)得L=$\frac{1}{cosθ}$+$\frac{1}{sinθ}$+$\frac{1}{sinθcosθ}$=$\frac{sinθ+cosθ+1}{sinθcosθ}$,
设sinθ+cosθ=t,则$sinθcosθ=\frac{{{t^2}-1}}{2}$,
∴L=$\frac{t+1}{\frac{{t}^{2}-1}{2}}$=$\frac{2}{t-1}$.
∵θ∈[$\frac{π}{6}$,$\frac{π}{3}$],t=sinθ+cosθ=$\sqrt{2}$sin(θ+$\frac{π}{4}$),
∴$\frac{1+\sqrt{3}}{2}$t≤$\sqrt{2}$.
当t=$\frac{1+\sqrt{3}}{2}$即θ=$\frac{π}{6}$或$\frac{π}{3}$时,L取得最大值2$\sqrt{3}$+2.
点评 本题考查了函数解析式的求解,三角函数的恒等变换与求值,属于中档题.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2015}{1008}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{4032}{2017}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
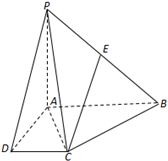 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2$\sqrt{2}$,PA=4且E为PB的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2$\sqrt{2}$,PA=4且E为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com