
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
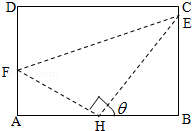 如图,矩形ABCD的内接Rt△FHE,(H是直角顶点),H是AB的中点,E,F分别落在线段BC,AD上.已知AB=2,AD=$\sqrt{3}$,记∠BHE=θ.
如图,矩形ABCD的内接Rt△FHE,(H是直角顶点),H是AB的中点,E,F分别落在线段BC,AD上.已知AB=2,AD=$\sqrt{3}$,记∠BHE=θ.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,有一圆锥形容器,其底面半径等于圆锥的高,若以72πcm3/s的速度向该容器注水,则水深10cm时水面上升的速度为$\frac{18}{25}$cm/s.
如图所示,有一圆锥形容器,其底面半径等于圆锥的高,若以72πcm3/s的速度向该容器注水,则水深10cm时水面上升的速度为$\frac{18}{25}$cm/s.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com