
���� ��1��ͨ�������ʣ�����ɵ�a2=3c2��b2=2c2����ֱ��FM�ķ���Ϊ$y=\frac{{\sqrt{3}}}{3}��{x+c}��$�����ù��ɶ��������ľʽ������ɵ�a2=3��b2=2����������Բ�ķ��̣�
��2���趯��P������Ϊ��x��y�����ֱ�����ֱ��FP��ֱ��OP����Բ���̣���x�ʣ�-$\frac{3}{2}$��-1����x�ʣ�-1��0������������ۼ��ɵó����ۣ�
��� �⣺��1������֪��$\frac{c^2}{a^2}=\frac{1}{3}$����a2=b2+c2���ɵ�a2=3c2��b2=2c2
��ֱ��FM�ķ���Ϊ$y=\frac{{\sqrt{3}}}{3}��{x+c}��$����Բ�ĵ�ֱ��FM�ľ��빫ʽ�ɵ�${d^2}={��{\frac{{\frac{{\sqrt{3}}}{3}c}}{{\sqrt{1+\frac{1}{3}}}}}��^2}=\frac{c^2}{4}⇒{d^2}+{��{\frac{c}{2}}��^2}=\frac{1}{2}⇒c=1$����a2=3��b2=2
���������Բ����Ϊ$\frac{x^2}{3}+\frac{y^2}{2}=1$��
��2�����P������Ϊ��x��y����ֱ��FP��б��Ϊt��FP��y=t��x+1����x��-1��
����$\left\{\begin{array}{l}y=t��{x+1}��\\ \frac{x^2}{3}+\frac{y^2}{2}=1\end{array}\right.$��ȥy����$2{x^2}+3{t^2}{��{x+1}��^2}=6⇒t=\sqrt{\frac{{6-2{x^2}}}{{3{{��{x+1}��}^2}}}}��\sqrt{2}$��
�ɽ��$-\frac{3}{2}��x��-1$��-1��x��0��
����ֱ��OP��б��Ϊ$m��⇒m=\frac{y}{x}��y=mx��{x��0}��$��
������$\left\{\begin{array}{l}y=mx\\ \frac{x^2}{3}+\frac{y^2}{2}=1\end{array}\right.⇒{m^2}=\frac{2}{x^2}-\frac{2}{3}$
�ٵ�$-\frac{3}{2}��x��-1$ʱ��y=t��x+1����0⇒m��0��$m=\sqrt{\frac{2}{x^2}-\frac{2}{3}}$��$m�ʣ�{\frac{{\sqrt{2}}}{3}��\frac{{2\sqrt{3}}}{3}}��$
�ڵ�-1��x��0ʱ��y=t��x+1����0⇒m��0��$m=-\sqrt{\frac{2}{x^2}-\frac{2}{3}}$��$m�ʣ�{-�ޣ�-\frac{{2\sqrt{3}}}{3}}��$
����ֱ��OP��б��m��ȡֵ��Χ$m�ʣ�{-�ޣ�-\frac{{2\sqrt{3}}}{3}}���ȣ�{\frac{{\sqrt{2}}}{3}��\frac{{2\sqrt{3}}}{3}}��$��
���� ���⿼����Բ�ı����̺ͼ������ʡ�ֱ�߷��̺�Բ�ķ��̡�ֱ����Բ��λ�ù�ϵ��һԪ���β���ʽ�Ȼ���֪ʶ�������ô��������о�Բ���ߵ����ʣ�������������������Լ��ú����뷽��˼��������������������е��⣮


 ��������������������ϵ�д�
��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
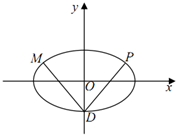 ��ͼ����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������e=$\frac{2\sqrt{2}}{3}$����ԲC���ҽ��㵽ֱ��x=$\frac{a}{e}$�ľ���Ϊ$\frac{\sqrt{2}}{4}$����ԲC���¶���ΪD��
��ͼ����ԲC��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������e=$\frac{2\sqrt{2}}{3}$����ԲC���ҽ��㵽ֱ��x=$\frac{a}{e}$�ľ���Ϊ$\frac{\sqrt{2}}{4}$����ԲC���¶���ΪD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2015}{1008}$ | B�� | $\frac{2017}{2016}$ | C�� | $\frac{2016}{2017}$ | D�� | $\frac{4032}{2017}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com