Question

11．定义运算M：x?y=$\left\{\begin{array}{l}|y|，x≥y\\ x，x＜y\end{array}$设函数f （x）=（x²-3）?（x-1），若函数y=f（x）-c恰有两个零点，则实数c的取值范围是（　　）

• A． （-3，-2）∪[2，+∞）
• B． （-1，0]∪（2，+∞）
• C． （-3，-2）
• D． （-1，0）

Answer 1

分析 现根据已知条件将函数f（x）化简出来，然后借助于数形结合的方法解决问题．

解答 解：由题意得f （x）=$\left\{\begin{array}{l}{1-x，x≤-1}\\{{x}^{2}-3，-1＜x＜2}\\{x-1，x≥2}\end{array}\right.$，作出函数f （x）的图象如图，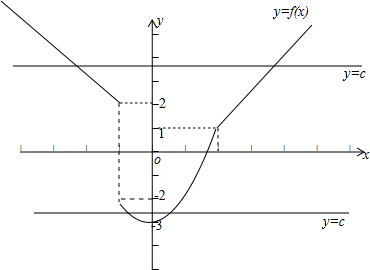

要使函数y=f （x）-c恰好有两个零点，即使函数y=f （x）与函数y=c的图象有两个交点，由图象可知，当c∈（-3，-2）∪[2，+∞）时，函数y=f （x）与函数y=c的图象有两个交点，即函数y=f （x）-c恰好有两个零点．
故选：A．

点评 本题是一个新定义问题，要注意正确理解“新运算”，然后利用数形结合的思想解决问题．