练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
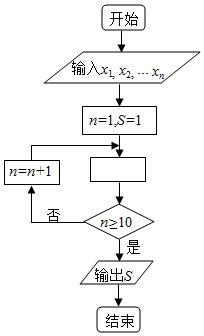
    10．如图是求x1，x2…x10的乘积S的程序框图，图中空白框中应填入的内容为（　　）
    A．S=S×（n+1）B．S=S×xn+1C．S=S×nD．S=S×xn

    分析 由题目要求可知：该程序的作用是求求x1，x2，…，x10的乘积，循环体的功能是累加各样本的值，故应为：S=S*xn．

    解答 解：由题目要求可知：该程序的作用是求求x1，x2，…，x10的乘积，
    结合流程图可得，
    循环体的功能是累乘各样本的值，
    故应为：S=S*xn，
    故选：D．

    点评 算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．其中前两点考试的概率更大．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．已知x、y满足约束条件$\left\{\begin{array}{l}x-y≥0\\ x+y-4≤0\\{（{x-2}）^2}+{y^2}≤4\end{array}\right.$，则z=-$\frac{{\sqrt{3}}}{3}$x+y的范围为$[{-2\sqrt{3}，2-\frac{{2\sqrt{3}}}{3}}]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知锐二面角α-l-β，A∈l，C∉l，C∈α，且AC⊥l，B∈l，D∉l，D∈β，BD⊥l．若$\overrightarrow{AC}$=（-2，1，-1），$\overrightarrow{BD}$=（-1，-1，-2），则二面角α-l-β的大小为（　　）
    A．$\frac{π}{6}$B．$\frac{π}{4}$C．$\frac{π}{3}$D．$\frac{5π}{12}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．如图，某园林单位准备绿化一块直径为BC的半圆形空地，△ABC外的地方种草，△ABC的内接正方形PQRS为一水池，其余的地方种花．若BC=a，∠ABC=θ，设△ABC的面积为S1，正方形PQRS的面积为S2．
    （1）用a，θ表示S1和S2；
    （2）当a为定值，θ变化时，求$\frac{{S}_{1}}{{S}_{2}}$的最小值，及此时的θ值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．第五届全国绿色运动健身大赛于2015年10月24日在安徽池州开赛．据了解，本届绿运健身大赛以“绿色池州、绿色运动、绿色生活”为主题．
    为调查某社区年轻人的周末生活状况，研究这一社区年轻人在周末的休闲方式与性别的关系，随机调查了该社区年轻人80人，得到下面的数据表：
            休闲方式
    性别    		 逛街上网  合计
     男 10 50 60
     女 10 10 20
     合计 20  6080 
    （1）根据以上数据，能否有99%的把握认为“周末年轻人的休闲方式与性别有关系”？
    （2）将此样本的频率估计为总体的概率，随机调查3名在该社区的年轻男生，设调查的3人在这一段时间以上网为休闲方式的人数为随机变量X，求X的分布列和数学期望．
    参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d
    参考数据：
     P（K2≥k0） 0.150.10  0.050.025  0.010
     k02.072  2.7063.841  5.0246.635 

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．在直角坐标系xOy中，曲线C1：$\left\{\begin{array}{l}x=\sqrt{3}+\frac{1}{2}t\\ y=2+\frac{{\sqrt{3}}}{2}t\end{array}$（t为参数），在以O为极点，x轴正半轴为极轴的极坐标系中，曲线C2：ρ=4．
    （Ⅰ）求出曲线C2的直角坐标方程；
    （Ⅱ）若C1与C2相交于A，B两点，求线段AB的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．直三棱柱ABC-A1B1C1中，AB⊥AC，AB=2，AC=4，AA1=2，D为BC的中点．则直线DB1与平面A1C1D所成角的正弦值$\frac{4}{15}\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立坐标系．已知曲线C的极坐标方程为ρ=2cosθ．直线l的参数方程为$\left\{\begin{array}{l}{x=\frac{\sqrt{2}}{2}t+2}\\{y=\frac{\sqrt{2}}{2}t}\end{array}\right.$（t为参数）．
    （1）求曲线C和直线l的普通方程方程；
    （2）设曲线C和直线l相交于A，B两点，求弦长|AB|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．一个几何体的三视图如图所示，其中正视图是圆心角为270°的扇形，俯视图与侧视图中圆的半径为2，则这个几何体的表面积是（　　）
    A．16πB．14πC．12πD．8π

    查看答案和解析>>

    同步练习册答案