
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 轴上方的点
轴上方的点![]() 在抛物线上,且
在抛物线上,且![]() ,直线
,直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点(点
两点(点![]() ,
,![]() 与
与![]() 不重合),设直线
不重合),设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
(Ⅰ)求抛物线的方程;
(Ⅱ)当![]() 时,求证:直线
时,求证:直线![]() 恒过定点并求出该定点的坐标.
恒过定点并求出该定点的坐标.
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:
【题目】从左到右依次写出1到10000的全部正整数,然后去掉那些能被5或7整除的数,将剩下的数连成一排组成一个新数。试求:
(1)新数的位数;
(2)新数被11除的余数。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市移动公司为了提高服务质量,决定对使用A,B两种套餐的集团用户进行调查,准备从本市![]() 个人数超过1000人的大集团和8个人数低于200人的小集团中随机抽取若干个集团进行调查,若一次抽取2个集团,全是小集团的概率为
个人数超过1000人的大集团和8个人数低于200人的小集团中随机抽取若干个集团进行调查,若一次抽取2个集团,全是小集团的概率为![]() .
.
![]() 求n的值;
求n的值;
![]() 若取出的2个集团是同一类集团,求全为大集团的概率;
若取出的2个集团是同一类集团,求全为大集团的概率;
![]() 若一次抽取4个集团,假设取出小集团的个数为X,求X的分布列和期望.
若一次抽取4个集团,假设取出小集团的个数为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为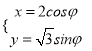 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求经过椭圆![]() 右焦点
右焦点![]() 且与直线
且与直线![]() 垂直的直线的极坐标方程;
垂直的直线的极坐标方程;
(2)若![]() 为椭圆
为椭圆![]() 上任意-点,当点
上任意-点,当点![]() 到直线
到直线![]() 距离最小时,求点
距离最小时,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况,随机抽取了100名观众,调查结果如下面的2×2列联表.
“非体育迷” | “体育迷” | 总计 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
总计 | 75 | 25 | 100 |
(1)据此资料判断是否有90%的把握认为“体育迷”与性别有关.
(2)将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”,已知“超级体育迷”共有5人,其中女性2名,男性3名,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是平面上由
是平面上由![]() 个点组成的点集.若在
个点组成的点集.若在![]() 中任取四个点,均至少有一个点与其余三个点相连,则下面结论中正确的是______.
中任取四个点,均至少有一个点与其余三个点相连,则下面结论中正确的是______.
①![]() 中不存在与其他所有点相连的点;
中不存在与其他所有点相连的点;
②![]() 中至少有一个点与其余所有的点均相连;
中至少有一个点与其余所有的点均相连;
③![]() 中至多有两个点与其余的点不相连;
中至多有两个点与其余的点不相连;
④![]() 中至多有两个点与其余所有的点均相连.
中至多有两个点与其余所有的点均相连.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com