
科目:高中数学 来源: 题型:选择题
| A. | 已知命题p,q,若p∨(¬q)为真命题,则q一定是假命题 | |
| B. | 命题“?x∈R,2x>0”的否定是“$?{x_0}∈R,{2^{x_0}}<0$” | |
| C. | “$x=\frac{π}{4}$”是“tan x=l”的充分不必要条件 | |
| D. | “若x1>1,x2>1,则x1+x2>2”的否命题是真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥底面ABCD,且∠ABC=$\frac{π}{2}$.
如图,在四棱柱ABCD-A1B1C1D1中,平面A1ABB1⊥底面ABCD,且∠ABC=$\frac{π}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
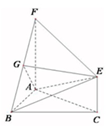 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF平行且等于2CE,G是线段BF上的一点,AB=AF=BC=2.
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF平行且等于2CE,G是线段BF上的一点,AB=AF=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
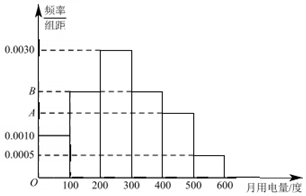 某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费.超过200度但不超过400度的部分按0.8 元/度收费,超过400度的部分按1.0 元/度收费.
某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费.超过200度但不超过400度的部分按0.8 元/度收费,超过400度的部分按1.0 元/度收费.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{2},+∞})$ | B. | )(0,+∞) | C. | (-1,+∞) | D. | .$({-\frac{1}{3},+∞})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com