
分析 (1)求导,由导数与函数单调性的关系,即可求得g(x)的单调区间;
(2)由g(e-a)=-a2+ea,构造函数h(x)=-x2+ex,求导,当x>e时,h′(x)>0,函数单调递增,即可求得h(x)=-x2+ex>-e2+ee>0,
(3)由(1)可知,函数最小值为g($\frac{1}{a}$)=0,故g(x)恰有两个零点x1,x2,则可判断x1,x2是函数的极大值和极小值,由函数零点的存在定理,求得函数f(x)只有一个零点.
解答 解:(1)对函数f(x),求导得g(x)=f′(x)=alnx+$\frac{1}{x}$,
g′(x)=$\frac{a}{x}$-$\frac{1}{{x}^{2}}$=$\frac{ax-1}{{x}^{2}}$,
①当a≤0时,g′(x)<0,故g(x)在(0,+∞)上为减函数;
②当a>0时,′(x)>0,可得x>$\frac{1}{a}$,故g(x)的减区间为(0,$\frac{1}{a}$),增区间为($\frac{1}{a}$,+∞);
(2)证明:g(e-a)=-a2+ea,设h(x)=-x2+ex,则h′(x)=ex-2x,
易知当x>e时,h′(x)>0,函数h(x)单调递增,
h(x)=-x2+ex>-e2+ee>0,
∴g(e-a)>0;
(3)由(1)可知,当a>e时,g(x)是先减再增的函数,
其最小值为g($\frac{1}{a}$)=aln$\frac{1}{a}$+a=a(ln$\frac{1}{a}$+1)<0,
而此时g(${e}^{\frac{1}{a}}$)=1+${e}^{\frac{1}{a}}$,g(e-a)>0,且e-a<$\frac{1}{a}$<${e}^{\frac{1}{a}}$,故g(x)恰有两个零点x1,x2,
∵当x∈(0,x1)时,f′(x)=g(x)>0;
当x∈(x1,x2)时,f′(x)=g(x)<0;
当x∈(x2,+∞)时,
f′(x)=g(x)>0,
∴f(x)在x1,x2两点分别取到极大值和极小值,且x1∈(0,$\frac{1}{a}$),
由g(x1)=alnx1+$\frac{1}{{x}_{1}}$=0,知a=-$\frac{1}{{x}_{1}ln{x}_{1}}$,
∴f(x1)=(ax1+1)lnx1-ax1+3=lnx1+$\frac{1}{ln{x}_{1}}$+2,
∵lnx1<0,∴lnx1+$\frac{1}{ln{x}_{1}}$≤-2,但当lnx1+$\frac{1}{ln{x}_{1}}$=-2时,lnx1=$\frac{1}{e}$,则a=e,不合题意,
所以f(x1)<0,故函数f(x)的图象与x轴不可能有两个交点.
∴函数f(x)只有一个零点.
点评 本题考查导数的综合应用,考查导数与函数的单调性及及的关系,考查函数零点的判断,考查计算能力,属于中档题.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:高中数学 来源: 题型:选择题
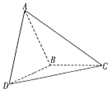 如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )
如图,在三棱锥A-BCD中,已知三角形ABC和三角形DBC所在平面互相垂直,AB=BD,∠CBA=∠CBD=$\frac{2π}{3}$,则直线AD与平面BCD所成角的大小是( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
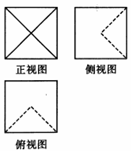
| A. | $20+4\sqrt{2}$ | B. | $24+4\sqrt{2}$ | C. | 24 | D. | 28 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{x}{2}$+$\frac{2}{x}$ | B. | y=lgx+$\frac{1}{lgx}$(1<x<10) | ||
| C. | y=3x+3-x(x∈R) | D. | y=sinx+$\frac{1}{sinx}$(0$<x<\frac{π}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com