已知椭圆
：
(
)过点
，其左、右焦点分别为
，且
．
（1）求椭圆的方程；
（2）若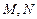
是直线
上的两个动点，且
，则以
为直径的圆
是否过定点？请说明理由．
科目：高中数学 来源：2014高考名师推荐数学文科选择题专项训练（解析版） 题型：选择题
全集U＝R，A＝{x|2x＞4}，B＝{x|log3x＜1}，则A∩B＝（ ）
A.{x|x＜－2} B.{x|2＜x＜3}
C.{x|x＞3} D.{x|x＜－2或2＜x＜3}
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科运用导数法确定函数的极值、最值、图像（解析版） 题型：选择题
函数f(x)的定义域为开区间(a，b)，导函数f′(x)在(a，b)内的图象如图所示，则函数f(x)在开区间(a，b)内有极小值点( )
A. 1个
B. 2个
C. 3个
D. 4个
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科证明不等式（解析版） 题型：选择题
设a,b,c,d∈R,若a+d=b+c,且|a-d|<|b-c|,则有 ( )
A. ad=bc
B. ad<bc
C. ad>bc
D. ad≤bc
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科解答题后三题（解析版） 题型：解答题
已知曲线
满足下列条件：
①过原点；②在
处导数为－1；③在
处切线方程为
.
(1) 求实数
的值；
（2）求函数的极值.
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科解答题前三题（解析版） 题型：解答题
如图，在四棱锥P—ABCD中，侧面PAD是正三角形，且垂直于底面ABCD，底面ABCD是边长为2的菱形，∠BAD=60°，M为PC的中点.
（1）求证：PA//平面BDM；
（2）求直线AC与平面ADM所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源：2014高考名师推荐数学文科空间直角坐标系简单应用（解析版） 题型：选择题
△ABC的顶点分别为A(1，－1，2)，B(5，－6，2)，C(1，3，－1)则AC边上的高BD等于( )
A．2
B．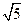
C．5
D．6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的坐标分别为
，
，可得
， 所以
，
，
的方程为
的坐标分别为
，则
，
，可得
，即
，又圆
的圆心为
半径为
，
， 即
，
， 令
，可得
或2，
和
．
。
，求
的单调区间；
时，
，求a的取值范围。
表示成θ＋2kπ(k∈Z)的形式，使|θ|最小的θ值是( )
