练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在四棱锥P—ABCD中，侧面PAD是正三角形，且垂直于底面ABCD，底面ABCD是边长为2的菱形，∠BAD=60°，M为PC的中点.

    （1）求证：PA//平面BDM；

    （2）求直线AC与平面ADM所成角的正弦值.

     

     

    （1）见解析      (2)

    【解析】证明：连结AC，交BD于点O,连结MO

    因为MO是的中位线，

    所以MO∥PA

    又因为面PAD中，

    所以MO∥面PAD（2）因为，点M到面ADC的距离，

    所以。

    因为为等腰三角形，且M为PC的中点,所以。

    取PB的中点E,AD的中点N，连结ME,PN,NE,BN

    因为四边形DMEN为平行四边形

    所以DM∥NE     又因为为等腰三角形，所以

    所以.

    因为，且

    所以面.

    所以。

    因为BC∥AD

    所以，因为

    所以

    所以

    所以

    所以．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：解答题

    已知椭圆，为坐标原点，椭圆的右准线与轴的交点是．

    （1）点在已知椭圆上，动点满足，求动点的轨迹方程；

    （2）过椭圆右焦点的直线与椭圆交于点，求的面积的最大值

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科运用导数解决实际问题（解析版） 题型：选择题

    某公司生产一种产品，固定成本为20000元，每生产一单位的产品，成本增加100元，若总收入R与年产量x的关系是，则当总利润最大时，每年生产产品的单位数是(　　)

    A. 150

    B. 200

    C. 250

    D. 300

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科解答题后三题（解析版） 题型：解答题

    已知椭圆：()过点，其左、右焦点分别为，且．

    （1）求椭圆的方程；

    （2）若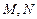是直线上的两个动点，且，则以为直径的圆是否过定点？请说明理由．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科解答题后三题（解析版） 题型：解答题

    证明以下不等式：

    (1)已知，，求证：；

    （2）若，，求证：.

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科解答题前三题（解析版） 题型：解答题

    三棱柱的直观图和三视图如下图所示，其侧视图为正三角形（单位cm）

    ⑴当x=4时，求几何体的侧面积和体积

    ⑵当x取何值时，直线AB1与平面BB1C1C和平面A1B1C1所成角大小相等。

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科解三角形（解析版） 题型：选择题

    在中，的对边分别为，若成等差数列，则(　　)

    A.

    B.

    C.

    D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科线性回归方程（解析版） 题型：选择题

    下表是某旅游区游客数量与平均气温的对比表：

    平均气温(℃)

    －1

    4

    10

    13

    18

    26

    数量(百个)

    20

    24

    34

    38

    50

    64

     

    若已知游客数量与平均气温是线性相关的，则回归方程为（    ）．

    A.＝1.98x＋22.13

    B.＝1.78x＋20.13

    C.＝1.68x＋18.73

    D.＝1.51x＋15.73

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科直线与圆锥曲线（解析版） 题型：选择题

    过抛物线y2＝2x的焦点F作直线交抛物线于A，B两点，若|AB|＝，|AF|<|BF|，则|AF|为（　　）

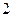    A. B. C. D.

     

    查看答案和解析>>

    同步练习册答案