
分析 (1)将m=1,a=0代入函数表达式,通过讨论x的范围,结合二次函数的性质,从而求出函数的单调性;
(2)将a=1代入函数的表达式,通过讨论x的范围,根据二次函数的性质,令f(x)=0,从而求出函数的零点,由题意讨论可求m的取值范围.
(3)将m=1,代入函数表达式,通过讨论x与a的大小的范围,去绝对值,求解g(x)=log2(4x)•log2$\frac{4}{x}$,在任意x∈(0,+∞)的值域M,讨论f(x)在R上函数的值域N,M⊆N从而求出a的取值范.
解答 解:(1)若m=1,a=0,则f(x)=x|x|-|x|+1=$\left\{\begin{array}{l}-{x}^{2}+x+1,x<0\\{x}^{2}-x+1,x≥0\end{array}\right.$,
根据二次函数的性质可得:
函数f(x)在(-∞,0)和($\frac{1}{2}$,+∞)上为增函数,在(0,$\frac{1}{2}$)上为减函数,
(2)若a=1,则f(x)=mx|x-1|-|x|+1=$\left\{\begin{array}{l}-{mx}^{2}+(m-1)x+1,x<0\\-{mx}^{2}+(m+1)x+1,0≤x≤1\\{mx}^{2}-(m+1)x+1,x>1\end{array}\right.$,
令f(x)=0,
当x<0时,解得:x=-$\frac{1}{m}$,或x=1(舍去),
当0≤x≤1时,解得:x=$\frac{-(m+1)±\sqrt{(m+1)^{2}+4m}}{-2m}$=$\frac{m+1±\sqrt{{m}^{2}+6m+1}}{2m}$,
当x>1时,解得:x=$\frac{1}{m}$,或x=1(舍去),
∵f(x)有且仅有一个零点,
①当m≥1时,x=-$\frac{1}{m}$为零点,x=$\frac{m+1±\sqrt{{m}^{2}+6m+1}}{2m}$不在[0,1]上,
即x1=$\frac{m+1+\sqrt{{m}^{2}+6m+1}}{2m}$>1,
x2=$\frac{m+1-\sqrt{{m}^{2}+6m+1}}{2m}$<0
解得:m>0,
∴m≥1,符合题意;
②0<m<1时,x=$\frac{1}{m}$为零点,根x=$\frac{m+1±\sqrt{{m}^{2}+6m+1}}{2m}$不在[0,1]上,满足题意.
∴0<m<1.
综上可得m的取值范围是(0,+∞).
(3)总存在x1∈R,对任意x2∈(0,+∞)恒有g(x2)<f(x1)-x12成立?总存在x1∈R,对任意x2∈(0,+∞)恒有:g(x2)max<$[f({x}_{1})-{x}_{1}^{2}]_{min}$.
函数g(x)=log2(4x)•log2$\frac{4}{x}$=(2+log2x)(2-log2x),
令t=log2x,x∈(0,+∞).
则t∈R.
那么函数h(t)=4-t2其值域为(-∞,4].即函数g(x)的值域M∈(-∞,4].∴g(x)max=4.
∵将m=1代入,可得:f(x)=x|x-a|-|x|+1
则f(x)-x2=x|x-a|-|x|+1-x2
当a=0时,由(1)可得:f(x)=$\left\{\begin{array}{l}{-2{x}^{2}+x+1,(x<0)}\\{-x+1,(x>0)}\end{array}\right.$
其f(x)的值域N为(-∞,0),不满足题意.
当a>0时,f(x)=$\left\{\begin{array}{l}{x(a-x)+x+1-{x}^{2},(x<0)}\\{x(a-x)-x+1-{x}^{2},(0≤x≤a)}\\{x(x-a)-x+1-{x}^{2},(x>a)}\end{array}\right.$,
点评 本题考查了函数的单调性问题,考查二次函数的性质,考查分类讨论思想,是一道中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
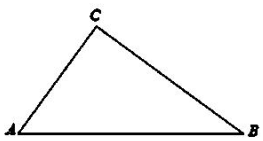 如图,A,B,C三地有直道相通,AB=10 千米,AC=6 千米,BC=8千米.现甲、乙两人同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为10千米/小时,乙的路线是ACB,速度为16千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
如图,A,B,C三地有直道相通,AB=10 千米,AC=6 千米,BC=8千米.现甲、乙两人同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为10千米/小时,乙的路线是ACB,速度为16千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=x2+2x|x-a|,其中a∈R.
已知函数f(x)=x2+2x|x-a|,其中a∈R.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{\sqrt{3}}{2}$,1) | B. | [$\frac{\sqrt{6}}{3}$,1) | C. | (0,$\frac{\sqrt{3}}{2}$] | D. | (0,$\frac{\sqrt{6}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$+y2=1 | B. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1 | C. | $\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{3}$+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com