
分析 (1)由已知条件利用指数性质及运算法则求解.
(2)由已知条件利用对数、指数的性质、运算法则求解.
解答 解:(1)(0.027)${\;}^{\frac{1}{3}}}$-(6$\frac{1}{4}}$)${\;}^{\frac{1}{2}}}$+π0-3-1
=[(0.3)3]${\;}^{\frac{1}{3}}$-($\frac{25}{4}$)${\;}^{\frac{1}{2}}$+1-$\frac{1}{3}$
=$\frac{3}{10}-\frac{5}{2}+\frac{2}{3}$
=-$\frac{23}{15}$.
(2)2log62+log69-log3$\frac{1}{9}$-8${\;}^{\frac{4}{3}}}$
=log64+log69-$lo{g}_{3}{3}^{-2}$-(23)${\;}^{\frac{4}{3}}$
=log636+2-24
=2+2-16
=-12.
点评 本题考查指数、对数化简求值,是基础题,解题时要认真审题,注意指数、对数的性质及运算法则的合理运用.


科目:高中数学 来源: 题型:解答题
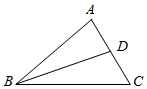 如图在△ABC中,AB=5,cos∠ABC=$\frac{1}{5}$.
如图在△ABC中,AB=5,cos∠ABC=$\frac{1}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | 34 | C. | 44 | D. | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{10}{3}$) | B. | (-∞,$\frac{10}{3}$] | C. | ($\frac{10}{3}$,+∞) | D. | (-∞,-$\frac{6}{5}$)∪(-$\frac{6}{5}$,$\frac{10}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{2}$ | B. | 2 | C. | 3 | D. | $\frac{11}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
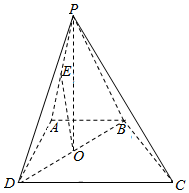 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,点O为BD的中点,E为PA的中点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,点O为BD的中点,E为PA的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com