
【题目】已知f(x)=ax﹣2 , g(x)=loga|x|(a>0且a≠1),若f(4)g(﹣4)<0,则y=f(x),y=g(x)在同一坐标系内的大致图象是( )
A.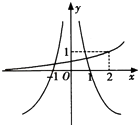
B.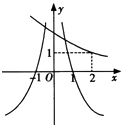
C.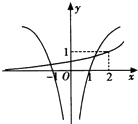
D.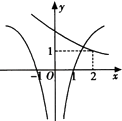
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】2016年奥运会于8月5日在巴西里约热内卢举行,为了解某单位员工对奥运会的关注情况,对本单位部分员工进行了调查,得到平均每天看奥运会直播时间的茎叶图如下(单位:分钟),若平均每天看奥运会直播不低于70分钟的员工可以视为“关注奥运”,否则视为“不关注奥运”.
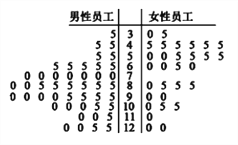
(1)试完成下面表格,并根据此数据判断是否有99.5%以上的把握认为是否“关注奥运会”与性别有关?
(2)若从参与调查且平均每天观看奥运会时间不低于110分钟的员工中抽取4人,用![]() 表示抽取的女员工数,求
表示抽取的女员工数,求![]() 的分布列和期望值.
的分布列和期望值.
参考公式: 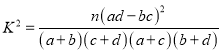 ,其中
,其中![]()
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
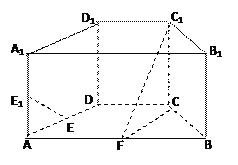
【题目】如图,在直四棱柱ABCD-A![]() B
B![]() C
C![]() D
D![]() 中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA
中,底面ABCD为等腰梯形,AB//CD,AB=4, BC=CD=2, AA![]() =2, E、E
=2, E、E![]() 、F分别是棱AD、AA
、F分别是棱AD、AA![]() 、AB的中点。
、AB的中点。
证明:(1)直线EE![]() //平面FCC
//平面FCC![]() ;
;
(2)求二面角B-FC![]() -C的余弦值。
-C的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞向月球,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行,若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
①a1+c1=a2+c2;②a1﹣c1=a2﹣c2;③c1a2>a1c2;④ ![]() .
.
其中正确式子的序号是( )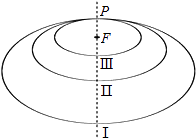
A.①③
B.②③
C.①④
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x+2 ![]() sin2x+1﹣
sin2x+1﹣ ![]() .
.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)当x∈[ ![]() ,
, ![]() ]时,求函数f(x)的值域.
]时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 的两个焦点为
的两个焦点为 ![]()
的曲线C上.
(1)求双曲线C的方程;
(2)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为2 ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检测某轮胎公司生产的轮胎的宽度,需要抽检一批轮胎(共10个轮胎),已知这批轮胎宽度(单位: ![]() )的折线图如下图所示:
)的折线图如下图所示:

(1)求这批轮胎宽度的平均值;
(2)现将这批轮胎送去质检部进行抽检,抽检方案是:从这批轮胎中任取5个作检验,这5个轮胎的宽度都在![]() 内,则称这批轮胎合格,如果抽检不合格,就要重新再抽检一次,若还是不合格,这批轮胎就认定不合格.
内,则称这批轮胎合格,如果抽检不合格,就要重新再抽检一次,若还是不合格,这批轮胎就认定不合格.
![]() 求这批轮胎第一次抽检就合格的概率;
求这批轮胎第一次抽检就合格的概率;
![]() 记
记![]() 为这批轮胎的抽检次数,求
为这批轮胎的抽检次数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生对“两个一百年”奋斗目标、实现中华民族伟大复兴中国梦的“关注度”(单位:天),某中学团委在全校采用随机抽样的方法抽取了80名学生(其中男女人数各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月“关注度”分为6组: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
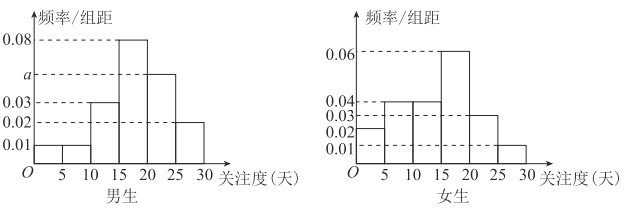
(1)求![]() 的值;
的值;
(2)求抽取的80名学生中月“关注度”不少于15天的人数;
(3)在抽取的80名学生中,从月“关注度”不少于25天的人中随机抽取2人,求至少抽取到1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com