Question

1．变量x，y满足约束条件$\left\{\begin{array}{l}{x+4y-13≥0}\\{2y-x+1≥0}\\{x+y-4≤0}\end{array}\right.$，且有无穷多个点（x，y）使目标函数z=x+my取得最小值，则m=（　　）

• A． -2
• B． -1
• C． 1
• D． 4

Answer 1

分析 先画出可行域，再研究目标函数，由于目标函数中含有参数m，故需讨论m的正负，再结合可行域，将目标函数赋予几何意义，数形结合确定满足题意的m的值

解答 解：画出可行域如图阴影区域：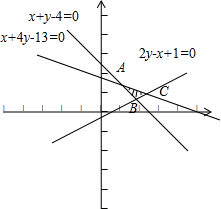
若m=0，则z=x，目标函数z=x+my取得最小值的最优解只有一个，不合题意
若m≠0，目标函数z=x+my可看做斜率为-$\frac{1}{m}$的动直线y=-$\frac{1}{m}$x+$\frac{z}{m}$
若m＜0，则-$\frac{1}{m}$＞0，数形结合知使目标函数z=x+my取得最小值的最优解不可能有无穷多个，
若m＞0，则-$\frac{1}{m}$＜0，数形结合可知，当动直线与直线AB平行时有无穷多个点（x，y）在线段AB上，使目标函数z=x+my取得最小值，
即-$\frac{1}{m}$=-1，m=1
故选：C．

点评 本题主要考查了线性规划的思想及其应用，可行域的画法及其应用，目标函数的意义，数形结合转化化归的思想方法，属中档题