
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| C | 1 n |
| C | 1 n |
| C | 2 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| C | 1 n |
| C | 1 n |
| C | 2 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| 1×(1-2n) |
| 1-2 |
| n |
 |
| i=1 |


 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
| A、从匀速传递的新产品生产流水线上,质检员每10分钟从中抽取一件新产品进行某项指标检测,这样的抽样是分层抽样 | ||
| B、样本方差反映了样本数据与样本平均值的偏离程度 | ||
| C、在回归分析模型中,残差平方和越小,说明模型的拟合效果越好 | ||
D、设随机变量X服从正态分布N(0,1),若P(x>1)=p,则P(-1<x<0)=
|
查看答案和解析>>
科目:高中数学 来源: 题型:
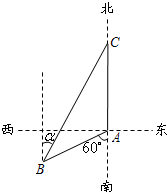 如图所示,海监船位于岛屿A的南偏西60°方向且与岛屿A相距12海里的B处,一艘不明身份的渔船从岛屿A出发沿正北方向以10海里/小时的速度航行.若海监船同时从B处出发,沿北偏东的方向以20海里/小时的速度尽快追赶渔船予以查处.则海监船最少约用多长时间能追上渔船?
如图所示,海监船位于岛屿A的南偏西60°方向且与岛屿A相距12海里的B处,一艘不明身份的渔船从岛屿A出发沿正北方向以10海里/小时的速度航行.若海监船同时从B处出发,沿北偏东的方向以20海里/小时的速度尽快追赶渔船予以查处.则海监船最少约用多长时间能追上渔船?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com