练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在直角坐标系xOy中,有一定点A(2,1),若线段OA的垂直平分线过抛物线y2=2px(p>0)的焦点,则该抛物线的准线方程是　　　　　　　　　　. 


    x=-

    解析:线段OA的斜率k=,中点坐标为.

    所以线段OA的垂直平分线的方程是

    y-=-2(x-1),

    令y=0得到x=.

    即抛物线的焦点为.

    所以该抛物线的准线方程为x=-.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知减函数f(x)的定义域是R,m,n∈R,如果不等式f(m)-f(n)>f(-m)-f(-n)成立,那么在下列给出的四个不等式中,正确的是(　　)

    (A)m+n<0    (B)m+n>0

    (C)m-n<0    (D)m-n>0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若二次函数f(x)=ax2+bx+c(a≠0)的图象和直线y=x无交点,现有下列结论:①方程f(f(x))=x一定没有实数根;

    ②若a>0,则不等式f(f(x))>x对一切实数x都成立;

    ③若a<0,则必存在实数x0,使f(f(x0))>x0;

    ④若a+b+c=0,则不等式f(f(x))<x对一切实数都成立;

    ⑤函数g(x)=ax2-bx+c的图象与直线y=-x也一定没有交点.

    其中正确的结论是　　　　(写出所有正确结论的编号). 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足,如果直线AF的斜率为-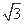,那么|PF|等于(　　)

    (A)4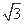 (B)8        (C)8 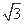(D)16

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示,在直角坐标系xOy中,点P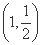到抛物线C:y2=2px(p>0)的准线的距离为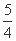.点M(t,1)是C上的定点,A,B是C上的两动点,且线段AB被直线OM平分.

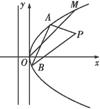
    (1)求p,t的值;

    (2)求△ABP面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知抛物线y2=4x的焦点为F,过F的直线与该抛物线相交于A(x1,y1)、B(x2,y2)两点,则+的最小值是(　　)

    (A)4    (B)8    (C)12   (D)16

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)=4x+ (x>0,a>0)在x=3时取得最小值,则a=　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设M是△ABC内一点,且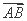·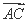=2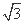,∠BAC=30°,定义f(M)=(m,n,p),其中m、n、p分别是△MBC、△MCA、△MAB的面积,若f(M)=(,x,y),则+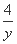的最小值是　　　　. 

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)=2sin(ωx+),x∈R,其中ω>0,-π<≤π.若f(x)的最小正周期为6π,且当x=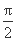时,f(x)取得最大值,则(　　)

    (A)f(x)在区间[-2π,0]上是增函数

    (B)f(x)在区间[-3π,-π]上是增函数

    (C)f(x)在区间[3π,5π]上是减函数

    (D)f(x)在区间[4π,6π]上是减函数

    查看答案和解析>>

    同步练习册答案