
【题目】下列命题:
①关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() 的系数行列式
的系数行列式![]() 是该方程组有解的必要非充分条件;
是该方程组有解的必要非充分条件;
②已知![]() 、
、![]() 、
、![]() 、
、![]() 是空间四点,命题甲:
是空间四点,命题甲:![]() 、
、![]() 、
、![]() 、
、![]() 四点不共面,命题乙:直线
四点不共面,命题乙:直线![]() 和
和![]() 不相交,则甲成立是乙成立的充分非必要条件;
不相交,则甲成立是乙成立的充分非必要条件;
③“![]() ”是“对任意的实数
”是“对任意的实数![]() ,
,![]() 恒成立”的充要条件;
恒成立”的充要条件;
④“![]() 或
或![]() ”是“关于
”是“关于![]() 的方程
的方程![]() 有且仅有一个实根”的充要条件;
有且仅有一个实根”的充要条件;
其中,真命题序号是________
【答案】②
【解析】
根据充分条件和必要条件的定义逐一判断,即可得出答案.
对于①,![]() 系数行列式
系数行列式![]() ,关于
,关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() 有唯一解,
有唯一解,
![]()
![]() 是该方程组有解的非充分条件
是该方程组有解的非充分条件
又![]() 系数行列式
系数行列式![]() ,
,![]() 或
或![]()
关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() 无解
无解
系数行列式![]() ,
, ![]()
关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() 有无穷组解
有无穷组解
![]() 关于
关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() 的系数行列式
的系数行列式![]() 是该方程组有解的非必要非充分条件;
是该方程组有解的非必要非充分条件;
故①不正确;
对于②,已知![]() 、
、![]() 、
、![]() 、
、![]() 是空间四点,命题甲:
是空间四点,命题甲:![]() 、
、![]() 、
、![]() 、
、![]() 四点不共面,命题乙:直线
四点不共面,命题乙:直线![]() 和
和![]() 不相交.
不相交.
![]() 命题甲可以推出命题乙,甲成立是乙成立的充分条件
命题甲可以推出命题乙,甲成立是乙成立的充分条件
又![]() 直线
直线![]() 和
和![]() 不相交,当
不相交,当![]() ,即
,即![]() 、
、![]() 、
、![]() 、
、![]() 四点共面,
四点共面,
![]() 命题乙不能推出命题甲,甲成立是乙成立的非必要条件
命题乙不能推出命题甲,甲成立是乙成立的非必要条件
![]() 甲成立是乙成立的充分非必要条件.
甲成立是乙成立的充分非必要条件.
故②正确;
对于③,设![]()
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
故![]()
![]()
![]() 能推出任意的实数
能推出任意的实数![]() ,
,![]()
又![]() 对任意的实数
对任意的实数![]() ,
,![]() 不能推出
不能推出![]()
故“![]() ”是“对任意的实数
”是“对任意的实数![]() ,
,![]() 恒成立”的充分不必要条件
恒成立”的充分不必要条件
故③不成立;
对于④,由关于![]() 的实系数方程
的实系数方程![]() 有且仅有一个实数根,得:
有且仅有一个实数根,得:![]() ,
,
由![]() 得:
得:![]() 或
或![]()
当![]() 时,得
时,得![]() ,检验知:
,检验知:![]() 不是方程
不是方程![]() 的实根,故此时方程无解
的实根,故此时方程无解
当![]() 时,
时,![]() ,解得
,解得![]() ,检验知:
,检验知:![]() 是方程
是方程![]() 的实根.
的实根.
故此时关于![]() 的方程
的方程![]() 有且仅有一个实数根
有且仅有一个实数根
![]() “
“![]() 或
或![]() ”不能推出“关于
”不能推出“关于![]() 的方程
的方程![]() 有且仅有一个实根”
有且仅有一个实根”
又![]() 关于
关于![]() 的方程
的方程![]() 有且仅有一个实根也不能推出“
有且仅有一个实根也不能推出“![]() 或
或![]() ”
”
![]() “
“![]() 或
或![]() ”是“关于
”是“关于![]() 的方程
的方程![]() 有且仅有一个实根”的既不充分也不必要条件.
有且仅有一个实根”的既不充分也不必要条件.
故④错误.
故答案为:②.


科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是圆
是圆![]() 的直径,
的直径,![]() ,
,![]() 在圆上且分别在
在圆上且分别在![]() 的两侧,其中
的两侧,其中![]() ,
,![]() .现将其沿
.现将其沿![]() 折起使得二面角
折起使得二面角![]() 为直二面角,则下列说法不正确的是( )
为直二面角,则下列说法不正确的是( )
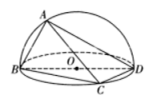
A.![]() ,
,![]() ,
,![]() ,
,![]() 在同一个球面上
在同一个球面上
B.当![]() 时,三棱锥
时,三棱锥![]() 的体积为
的体积为![]()
C.![]() 与
与![]() 是异面直线且不垂直
是异面直线且不垂直
D.存在一个位置,使得平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且(2b-c)cos A=acos C.
(1)求角A的大小;
(2)若a=3,b=2c,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角梯形![]() 与等腰直角三角形
与等腰直角三角形![]() 所在的平面互相垂直.
所在的平面互相垂直.![]() ,
,![]() ,
,![]() ,
,![]() .
.
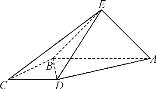
(1) 求证:![]() ;
;
(2) 求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3) 线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]()
![]() 若存在,求出
若存在,求出![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的12月4日为我国“法制宣传日”.天津市某高中团委在2019年12月4日开展了以“学法、遵法、守法”为主题的学习活动.已知该学校高一、高二、高三的学生人数分别是480人、360人、360人.为检查该学校组织学生学习的效果,现采用分层抽样的方法从该校全体学生中选取10名学生进行问卷测试.具体要求:每位被选中的学生要从10个有关法律、法规的问题中随机抽出4个问题进行作答,所抽取的4个问题全部答对的学生将在全校给予表彰.
⑴求各个年级应选取的学生人数;
⑵若从被选取的10名学生中任选3人,求这3名学生分别来自三个年级的概率;
⑶若被选取的10人中的某学生能答对10道题中的7道题,另外3道题回答不对,记![]() 表示该名学生答对问题的个数,求随机变量
表示该名学生答对问题的个数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=1+λan,其中λ≠0.
(1)证明{an}是等比数列,并求其通项公式;
(2)当λ=2时,求数列{![]() }的前n项和.
}的前n项和.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com