
【题目】每年的12月4日为我国“法制宣传日”.天津市某高中团委在2019年12月4日开展了以“学法、遵法、守法”为主题的学习活动.已知该学校高一、高二、高三的学生人数分别是480人、360人、360人.为检查该学校组织学生学习的效果,现采用分层抽样的方法从该校全体学生中选取10名学生进行问卷测试.具体要求:每位被选中的学生要从10个有关法律、法规的问题中随机抽出4个问题进行作答,所抽取的4个问题全部答对的学生将在全校给予表彰.
⑴求各个年级应选取的学生人数;
⑵若从被选取的10名学生中任选3人,求这3名学生分别来自三个年级的概率;
⑶若被选取的10人中的某学生能答对10道题中的7道题,另外3道题回答不对,记![]() 表示该名学生答对问题的个数,求随机变量
表示该名学生答对问题的个数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(1)高一年级应选取![]() 人,高二年级应选取
人,高二年级应选取![]() 人,高三年级应选取
人,高三年级应选取![]() 人.(2)
人.(2)![]() (3)详见解析
(3)详见解析
【解析】
(1)利用分层抽样求得各年级应抽取的人数;
(2)利用计算原理求得基本事件的总数为![]() ,再求出所求事件的基本事件数,再代入古典概型概率计算公式;
,再求出所求事件的基本事件数,再代入古典概型概率计算公式;
(3)随机变量![]() 的所有可能取值为
的所有可能取值为![]() ,利用超几何分计算
,利用超几何分计算 (
(![]() ),最后求得期望值.
),最后求得期望值.
(1)由题意,知高一、高二、高三年级的人数之比为![]() ,由于采用分层抽样方法从中选取
,由于采用分层抽样方法从中选取![]() 人,因此,高一年级应选取
人,因此,高一年级应选取![]() 人,高二年级应选取
人,高二年级应选取![]() 人,高三年级应选取
人,高三年级应选取![]() 人.
人.
(2)由(1)知,被选取的![]() 名学生高一、高二、高三年级分别有
名学生高一、高二、高三年级分别有![]() 人、
人、![]() 人、
人、![]() 人,所以,从这
人,所以,从这![]() 名学生任选
名学生任选![]() 名,且
名,且![]() 名学生分别来自三个年级的概率为
名学生分别来自三个年级的概率为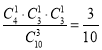 .
.
(3)由题意知,随机变量![]() 的所有可能取值为
的所有可能取值为![]() ,
,
且![]() 服从超几何分布,
服从超几何分布, (
(![]() ).
).
所以,随机变量![]() 的分布列为
的分布列为
| 1 | 2 | 3 | 4 |
|
|
|
|
|
所以,随机变量![]() 的数学期望为
的数学期望为
![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且AB=1,BC=2, ∠ABC=60°,PA⊥平面ABCD,AE⊥PC于E,
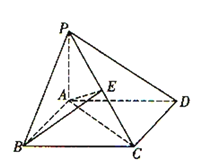
下列四个结论:①AB⊥AC;②AB⊥平面PAC;③PC⊥平面ABE;④BE⊥PC.正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() 的系数行列式
的系数行列式![]() 是该方程组有解的必要非充分条件;
是该方程组有解的必要非充分条件;
②已知![]() 、
、![]() 、
、![]() 、
、![]() 是空间四点,命题甲:
是空间四点,命题甲:![]() 、
、![]() 、
、![]() 、
、![]() 四点不共面,命题乙:直线
四点不共面,命题乙:直线![]() 和
和![]() 不相交,则甲成立是乙成立的充分非必要条件;
不相交,则甲成立是乙成立的充分非必要条件;
③“![]() ”是“对任意的实数
”是“对任意的实数![]() ,
,![]() 恒成立”的充要条件;
恒成立”的充要条件;
④“![]() 或
或![]() ”是“关于
”是“关于![]() 的方程
的方程![]() 有且仅有一个实根”的充要条件;
有且仅有一个实根”的充要条件;
其中,真命题序号是________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊数学家阿波罗尼斯在其巨著《圆锥曲线论》中提出“在同一平面上给出三点,若其中一点到另外两点的距离之比是一个大于零且不等于1的常数,则该点轨迹是一个圆”现在,某电信公司要在甲、乙、丙三地搭建三座5G信号塔来构建一个三角形信号覆盖区域,以实现5G商用,已知甲、乙两地相距4公里,丙、甲两地距离是丙、乙两地距离的![]() 倍,则这个三角形信号覆盖区域的最大面积(单位:平方公里)是( )
倍,则这个三角形信号覆盖区域的最大面积(单位:平方公里)是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥![]() 底面是直角梯形,点E是棱PC的中点,
底面是直角梯形,点E是棱PC的中点,![]() ,
,![]() 底面ABCD,
底面ABCD,![]() .
.
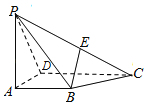
(1)判断BE与平面PAD是否平行,证明你的结论;
(2)证明:![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积V.
的体积V.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() , 过点
, 过点![]() 的直线
的直线![]() :
:![]() 与椭圆
与椭圆![]() 交于M、N两点(M点在N点的上方),与
交于M、N两点(M点在N点的上方),与![]() 轴交于点E.
轴交于点E.
(1)当![]() 且
且![]() 时,求点M、N的坐标;
时,求点M、N的坐标;
(2)当![]() 时,设
时,设![]() ,
,![]() ,求证:
,求证:![]() 为定值,并求出该值;
为定值,并求出该值;
(3)当![]() 时,点D和点F关于坐标原点对称,若△MNF的内切圆面积等于
时,点D和点F关于坐标原点对称,若△MNF的内切圆面积等于![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com