练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知函数$f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜\frac{π}{2}）$的周期为π，若f（α）=1，则$f（α+\frac{3π}{2}）$=（　　）
    A．-2B．-1C．1D．2

    分析 根据函数f（x）的周期求出ω的值，再化简f（α+$\frac{3π}{2}$）并求值．

    解答 解：因为函数f（x）=Asin（ωx+φ）的周期为
    T=$\frac{2π}{ω}$=π，∴ω=2，
    ∴f（x）=Asin（2x+φ），
    又f（α）=Asin（2α+φ）=1，
    ∴f（α+$\frac{3π}{2}$）=Asin[2（α+$\frac{3π}{2}$）+φ]
    =Asin（2α+3π+φ）
    =-Asin（2α+φ）
    =-1．
    故选：B．

    点评 本题考查了三角函数的图象与性质的应用问题，是基础题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．函数$y=\sqrt{3-x}$的定义域为（-∞，3]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．在四面体ABCD中，AB⊥AD，AB=AD=BC=CD=1，且平面ABD⊥平面BCD，M为AB中点，则线段CM的长为（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．$\frac{\sqrt{3}}{2}$D．$\frac{\sqrt{2}}{2}$

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年河北省保定市高一上学期期中考试数学试卷（解析版） 题型：选择题

    如图①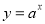，②，③，④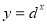，根据图象可得a、b、c、d与1的大小关系为（ ）

    A．a＜b＜1＜c＜d B．b＜a＜1＜d＜c

    C．1＜a＜b＜c＜d D．a＜b＜1＜d＜c

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知全集U=R，集合A={x|x＞2}，B={1，2，3，4}，那么（∁UA）∩B=（　　）
    A．{3，4}B．{1，2，3}C．{1，2}D．{1，2，3，4}

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

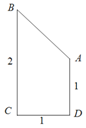    7．如图，直角梯形ABCD中，AD⊥DC，AD∥BC，BC=2CD=2AD=2，若将直角梯形绕BC边旋转一周，则所得几何体的表面积为$（3+{\sqrt{2}^{\;}}）π$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．如图所示，在正方体ABCD-A1B1C1D1中，已知M，N分别是BD和AD的中点，则B1M与D1N所成角的余弦值为（　　）
    A．$\frac{{\sqrt{30}}}{10}$B．$\frac{{\sqrt{30}}}{15}$C．$\frac{{\sqrt{30}}}{30}$D．$\frac{{\sqrt{15}}}{15}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知集合A={x|2x2-3x+1≤0}，集合B={x|x2-（2a+1）x+a（a+1）≤0}．若A⊆B，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知sin（π-α）-2sin（$\frac{π}{2}$+α）=0．
    （1）求sinαcosα+sin2α的值．
    （2）若tan（α+β）=-1，求tanβ的值．

    查看答案和解析>>

    同步练习册答案