
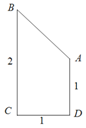
 如图,直角梯形ABCD中,AD⊥DC,AD∥BC,BC=2CD=2AD=2,若将直角梯形绕BC边旋转一周,则所得几何体的表面积为$(3+{\sqrt{2}^{\;}})π$.
如图,直角梯形ABCD中,AD⊥DC,AD∥BC,BC=2CD=2AD=2,若将直角梯形绕BC边旋转一周,则所得几何体的表面积为$(3+{\sqrt{2}^{\;}})π$. 分析 由圆锥及圆柱的几何特征可得,该几何体由两个底面相待的圆锥和圆柱组合而成,其中圆柱和圆锥的高均为1,代入圆柱和圆锥的体积公式,即可得到答案.
解答 解:由图中数据可得:${S_{圆锥侧}}=\frac{1}{2}×π×2×\sqrt{2}=\sqrt{2}π$,S圆柱侧=π×2×1=2π,${S_{底面}}=π×{1^2}=π$.
所以几何体的表面积为${S_{表面积}}=(3+{\sqrt{2}^{\;}})π$.
故答案为:$(3+{\sqrt{2}^{\;}})π$.
点评 本题考查的知识点是圆柱与圆锥的体积及余弦定理,关键是:(1)熟练掌握圆柱和圆锥的体积公式是关键,(2)将空间问题转化为平面问题是解答立体几何常用的技巧.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
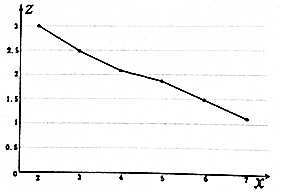
| 使用年数x | 2 | 3 | 4 | 5 | 6 | 7 |
| 售价y | 20 | 12 | 8 | 6.4 | 4.4 | 3 |
| z=lny | 3.00 | 2.48 | 2.08 | 1.86 | 1.48 | 1.10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y与x具有正线性相关关系 | |
| B. | 回归直线过样本的中心点$(\overline x,\overline y)$ | |
| C. | 若该中学某高中女生身高增加1cm,则其体重约增加0.85kg | |
| D. | 若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 16 | C. | 32 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 0 | 1 | 3 | 5 | 6 |
| y | 1 | m | 3m | 5.6 | 7.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com