
 为该顾客摸球停止时所得的奖金数,求
为该顾客摸球停止时所得的奖金数,求 的分布列及均值.
的分布列及均值.科目:高中数学 来源:不详 题型:解答题
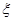 .
.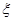 的分布列;
的分布列;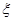 的数学期望);
的数学期望); ,一等品率提高为
,一等品率提高为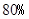 .如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于5.13万元,则三等品率最多是多少?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 .
. ,试写出
,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 参加次数 | 0 | 1 | 2 | 3 |
| 人数 | 0.1 | 0.2 | 0.4 | 0.3 |
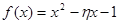 在区间
在区间 ,
, 内有零点”的事件为
内有零点”的事件为 ,求
,求 发生的概率
发生的概率 ;
;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
 表示销售一套该户型住房的利润。
表示销售一套该户型住房的利润。 的分布列及数学期望E
的分布列及数学期望E .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 动作 | K | D | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 |  |  |  |  |
| 动作 | K | D | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 |  |  |  |  |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com