【题目】有下列命题：①边长为1的正四面体的内切球半径为
；
②正方体的内切球、棱切球（正方体的每条棱都与球相切）、外接球的半径之比为1：
；
③棱长为1的正方体ABCD-A1B1C1D1的内切球被平面A1BD截得的截面面积为
．
其中正确命题的序号是______（请填所有正确命题的序号）；
【答案】①②③
【解析】
运用正四面体的性质和体积公式，结合等积法可得球的半径，可判断①；
由正方体与内切球、棱切球和外接球的关系，求得半径，可判断②；
求得正方体内切球半径，结合球的截面性质，以及勾股定理和等边三角形的性质，即可判断③．
①边长为1的正四面体的高为h
，
可得正四面体的体积为V
h
，
设内切球的半径为r，由等积法可得VrSr4，（S为正四面体的全面积）
解得r
，故①正确；
②设边长为1的正方体的内切球、棱切球（正方体的每条棱都与球相切）、外接球的半径
分别为r1，r2，r3，可得2r1＝1，2r2
，2r3
，
即有r1：r2：r3＝1：
，故②正确；
③棱长为1的正方体ABCD﹣A1B1C1D1的内切球的半径为
，
设内心为I，可得A1I
，I在截面的射影为等边三角形A1BD的中心O，
可得OI
，
由球的截面的性质可得截面圆的半径为
，可得截面圆的面积为
，故③正确．
故答案为：①②③．
科目：高中数学 来源： 题型：
【题目】2017年“双节”期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速
分成六段： 
， 
， 
， 
， 
， 
后得到如图的频率分布直方图．
（1）调查公司在采样中，用到的是什么抽样方法？
（2）求这40辆小型车辆车速的众数、中位数及平均数的估计值；
（3）若从车速在
的车辆中任抽取2辆，求车速在的车辆至少有一辆的概率．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，平面中两条直线
和
相交于点O，对于平面上任意一点M，若p，q分别是M到直线和的距离，则称有序非负实数对
是点M的“距离坐标”.下列四个命题中正确命题为( )
A.若
，则“距离坐标”为
的点有且仅有1个
B.若
，且
，则“距离坐标”为的点有且仅有2个
C.若
，则“距离坐标”为的点有且仅有4个
D.若
，则点M在一条过点O的直线上
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知等腰直角三角形
的斜边
所在直线方程为
，其中
点在
点上方，直角顶点
的坐标为
．
（1）求边上的高线
所在直线的方程；
（2）求等腰直角三角形的外接圆的标准方程；
（3）分别求两直角边
，
所在直线的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知在平面直角坐标系中，直线l过点P（1，2）．
（1）若直线l在x轴和y轴上的截距相等，求直线l的方程；
（2）求坐标原点O到直线l距离取最大值时的直线l的方程；
（3）设直线l与x轴正半轴、y轴正半轴分别相交于A，B两点，当|PA||PB|最小时，求直线l的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱ABC-A1B1C1中，△ABC和△AA1C均是边长为2的等边三角形，点O为AC中点，平面AA1C1C⊥平面ABC．
（1）证明：A1O⊥平面ABC；
（2）求直线AB与平面A1BC1所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，直线
的参数方程为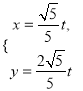
（
为参数），以平面直角坐标系的原点为极点，正半轴为极轴，取相同的长度单位建立极坐标系，曲线
的极坐标方程为
.
（1）求直线
和曲线
的直角坐标方程，并指明曲线
的形状；
（2）设直线
与曲线
交于
两点， 
为坐标原点，且
，求
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
