
分析 利用圆的参数方程,确定Q,R的坐标,求出QR,即可求线段RQ长度的最大值和最小值.
解答 解:由题意,设P(3+$\frac{5}{2}$cosθ,3+$\frac{5}{2}$sinθ),(θ为参数,0≤θ<2π),
∵P关于点A(7,0)的对称点为Q,
∴Q(11-$\frac{5}{2}$cosθ,-3-$\frac{5}{2}$sinθ)
∵把点P绕圆心C(3,3)逆时针方向转过120°后得点R,
∴R(3+$\frac{5}{2}$cos(θ+120°),3+$\frac{5}{2}$sin(θ+120°))
∴|QR|2=($\frac{5}{4}$cosθ-$\frac{5}{4}\sqrt{3}$sinθ-8)2+($\frac{5}{4}$sinθ+$\frac{5}{4}\sqrt{3}$cosθ+6)2=$\frac{425}{4}$+50sin(θ+α)
∴|QR|的最大值为$\frac{25}{2}$,|QR|的最小值为$\frac{15}{2}$.
点评 本题考查圆的参数方程,考查三角函数知识,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | l垂直于平面α内的一条直线 | B. | l垂直于平面α内的两条直线 | ||
| C. | l垂直于平面α内的无数条直线 | D. | l垂直于平面α内的任一条直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{8}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{4-π}{8}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 过定点(4p,0) | B. | 过定点(2p,0) | C. | 过定点(p,0) | D. | 过抛物线焦点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)在区间[0,$\frac{π}{2}$]内是增函数 | |
| B. | 若?x1≠x2,f(x1)=f(x2)=0,则x1-x2必是π的整数倍 | |
| C. | f(x)的图象关于点(-$\frac{π}{12}$+$\frac{kπ}{2}$,0)(k∈Z)对称 | |
| D. | f(x)的图象关于直线x=$\frac{π}{12}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ①② | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
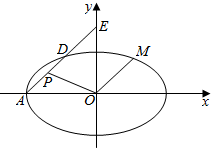 如图,在平面直角坐标系xoy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
如图,在平面直角坐标系xoy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com