
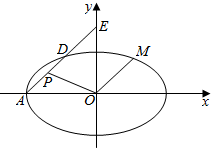
 ��ͼ����ƽ��ֱ������ϵxoy�У���֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0����������e=$\frac{1}{2}$����ΪA��-4��0��������A��б��Ϊk��k��0����ֱ��l����ԲC�ڵ�D����y���ڵ�E��
��ͼ����ƽ��ֱ������ϵxoy�У���֪��ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0����������e=$\frac{1}{2}$����ΪA��-4��0��������A��б��Ϊk��k��0����ֱ��l����ԲC�ڵ�D����y���ڵ�E������ ��1������Բ�������ʺ��㣬���a��b���ɴ��������ԲC�ı����̣�
��2��ֱ��l�ķ���Ϊy=k��x+4��������Բ�������ã���x+4��[��4k2+3��x+16k2-12��]=0���ɴ�����Τ�ﶨ����ֱ�ߴ�ֱ�������������������
��3��OM�ķ��̿���Ϊy=kx������Բ������M��ĺ�����Ϊ$x=��\frac{{4\sqrt{3}}}{{\sqrt{4{k^2}+3}}}$����OM��l������������
��� �⣺��1������ԲC��$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1��a��b��0����������e=$\frac{1}{2}$����ΪA��-4��0����
��a=4����$e=\frac{1}{2}$����c=2������2�֣�
�֡�b2=a2-c2=12��
����ԲC�ı�����Ϊ$\frac{x^2}{16}+\frac{y^2}{12}=1$������4�֣�
��2��ֱ��l�ķ���Ϊy=k��x+4����
��$\left\{\begin{array}{l}\frac{x^2}{16}+\frac{y^2}{12}=1\\ y=k��x+4��\end{array}\right.$��Ԫ�ã�$\frac{x^2}{16}+\frac{{{{[k��x+4��]}^2}}}{12}=1$��
������x+4��[��4k2+3��x+16k2-12��]=0��
��x1=-4��${x_2}=\frac{{-16{k^2}+12}}{{4{k^2}+3}}$������6�֣�
��$x=\frac{{-16{k^2}+12}}{{4{k^2}+3}}$ʱ��$y=k��\frac{{-16{k^2}+12}}{{4{k^2}+3}}+4��=\frac{24k}{{4{k^2}+3}}$��
��$D��\frac{{-16{k^2}+12}}{{4{k^2}+3}}��\frac{24k}{{4{k^2}+3}}��$��
�ߵ�PΪAD���е㣬��P������Ϊ$��\frac{{-16{k^2}}}{{4{k^2}+3}}��\frac{12k}{{4{k^2}+3}}��$��
��${k_{OP}}=-\frac{3}{4k}��k��0��$������8�֣�
ֱ��l�ķ���Ϊy=k��x+4������x=0����E������Ϊ��0��4k����
������ڶ���Q��m��n����m��0����ʹ��OP��EQ��
��kOPkEQ=-1����$-\frac{3}{4k}•\frac{n-4k}{m}=-1$�������
�ࣨ4m+12��k-3n=0���������$\left\{\begin{array}{l}4m+12=0\\-3n=0\end{array}\right.$����$\left\{\begin{array}{l}m=-3\\ n=0\end{array}\right.$��
�ඨ��Q������Ϊ��-3��0��������10�֣�
��3����OM��l����OM�ķ��̿���Ϊy=kx��
��$\left\{\begin{array}{l}\frac{x^2}{16}+\frac{y^2}{12}=1\\ y=kx\end{array}\right.$����M��ĺ�����Ϊ$x=��\frac{{4\sqrt{3}}}{{\sqrt{4{k^2}+3}}}$������12�֣�
��OM��l����$\frac{AD+AE}{OM}=\frac{{|{{x_D}-{x_A}}|+|{{x_E}-{x_A}}|}}{{|{x_M}|}}=\frac{{{x_D}-2{x_A}}}{{|{x_M}|}}$
=$\frac{{\frac{{-16{k^2}+12}}{{4{k^2}+3}}+8}}{{\frac{{4\sqrt{3}}}{{\sqrt{4{k^2}+3}}}}}=\frac{1}{{\sqrt{3}}}•\frac{{4{k^2}+9}}{{\sqrt{4{k^2}+3}}}$����14�֣�
=$\frac{1}{{\sqrt{3}}}��\sqrt{4{k^2}+3}+\frac{6}{{\sqrt{4{k^2}+3}}}����2\sqrt{2}$��
���ҽ���$\sqrt{4{k^2}+3}=\frac{6}{{\sqrt{4{k^2}+3}}}$��$k=��\frac{{\sqrt{3}}}{2}$ʱȡ�Ⱥţ�
�൱$k=��\frac{{\sqrt{3}}}{2}$ʱ��$\frac{AD+AE}{OM}$����СֵΪ$2\sqrt{2}$�� ����16�֣�
���� ���⿼����Բ���̵����������������Ķ����Ƿ���ڵ��ж������������ʽ����Сֵ�������е��⣬����ʱҪ�������⣬ע��Τ�ﶨ����ֱ�ߴ�ֱ����Բ���ʵĺ������ã�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| ��Ʒ�� | 0 | 1 | 2 | 3 | 4 |
| Ƶ�� | 0.5 | 0.2 | 0.05 | 0.2 | 0.05 |
| A�� | 0��1.1 | B�� | 0��1 | C�� | 4��1 | D�� | 0.5��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com