
| 次品数 | 0 | 1 | 2 | 3 | 4 |
| 频率 | 0.5 | 0.2 | 0.05 | 0.2 | 0.05 |
| A. | 0,1.1 | B. | 0,1 | C. | 4,1 | D. | 0.5,2 |
科目:高中数学 来源: 题型:选择题
| A. | f(x)在区间[0,$\frac{π}{2}$]内是增函数 | |
| B. | 若?x1≠x2,f(x1)=f(x2)=0,则x1-x2必是π的整数倍 | |
| C. | f(x)的图象关于点(-$\frac{π}{12}$+$\frac{kπ}{2}$,0)(k∈Z)对称 | |
| D. | f(x)的图象关于直线x=$\frac{π}{12}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
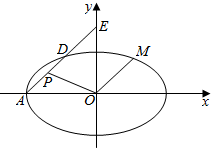 如图,在平面直角坐标系xoy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
如图,在平面直角坐标系xoy中,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率e=$\frac{1}{2}$,左顶点为A(-4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
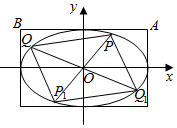 (重点中学做)已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,1),离心率e=$\frac{\sqrt{6}}{3}$
(重点中学做)已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,1),离心率e=$\frac{\sqrt{6}}{3}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
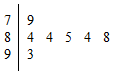 如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
如图,是2007年在广州举行的全国少数民族运动会上,七位评委为某民族舞蹈打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )| A. | 84,4.84 | B. | 84,1.6 | C. | 85,2.4 | D. | 85,1.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com