
【题目】如图1,在直角梯形ABCD中,AB∥CD,∠DAB=90°,点E、F分别在CD、AB上,且EF⊥CD,BE⊥BC,BC=1,CE=2.现将矩形ADEF沿EF折起,使平面ADEF与平面EFBC垂直(如图2). 
(1)求证:CD∥面ABF;
(2)当AF的长为何值时,二面角A﹣BC﹣F的大小为30°.
【答案】
(1)证明:∵CE∥BF,CE面ABF,BF面ABF,
∴CE∥面ABF,
又DE∥AF,DE面ABF,AF面ABF,
∴DE∥面ABF,
∵DE∩CE=E,且DE、CE面CDE,
∴面CDE∥面ABF,
又CD面CDE,∴CD∥面ABF.
(2)解:过F作CB的垂线,交CB的延长线于H点,连结AH,
∵面ADEF⊥面EFBC,AF⊥EF,
∴AF⊥面EFBC,CB面EFBC,
∴CB⊥AF,CB⊥面AF,
∴AH⊥CH,
∴∠AHF是二面角A﹣BC﹣F的平面角,
∴∠AHF=30°,
∵BC=1,CE=2,且BE⊥BC,∴∠BCE=60°,
在直线梯形EFBC中,BF=2﹣cos60°= ![]() ,
,
∴FH= ![]() =
= ![]() ,
,
在直角三角形AHF中,AF=FH ![]() .
.

【解析】(1)推导出CE∥面ABF,DE∥面ABF,由此能证明面CDE∥面ABF,从而CD∥面ABF.(2)过F作CB的垂线,交CB的延长线于H点,连结AH,推导出∠AHF是二面角A﹣BC﹣F的平面角,由此能求出AF的长.
【考点精析】通过灵活运用直线与平面平行的判定,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行即可以解答此题.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).
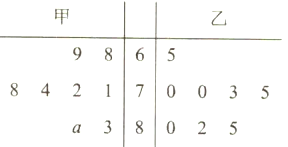
(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x-P2-x,则下列结论正确的是( )
A. ![]() ,
,![]() 为奇函数且为R上的减函数
为奇函数且为R上的减函数
B. ![]() ,
,![]() 为偶函数且为R上的减函数
为偶函数且为R上的减函数
C. ![]() ,
,![]() 为奇函数且为R上的增函数
为奇函数且为R上的增函数
D. ![]() ,
,![]() 为偶函数且为R上的增函数
为偶函数且为R上的增函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c.若sin(A﹣B)+sinC= ![]() sinA.
sinA.
(1)求角B的值;
(2)若b=2,求a2+c2的最大值,并求取得最大值时角A,C的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意度进行调查,并随机抽取了其中30名员工(其中16名女员工,14名男员工)的得分,如下表:
女 | 47 36 32 48 34 44 43 47 46 41 43 42 50 43 35 49 |
男 | 37 35 34 43 46 36 38 40 39 32 48 33 40 34 |
(Ⅰ)现求得这30名员工的平均得分为40.5分,若规定大于平均得分为“满意”,否则为“不满意”,请完成下列表格:
“满意”的人数 | “不满意”的人数 | 合计 | |
女 | 16 | ||
男 | 14 | ||
合计 | 30 |
(Ⅱ)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?
参考数据:
| 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考公式:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题中:
①命题“若x≥2且y≥3,则x+y≥5”为假命题.
②命题“若x2-4x+3=0,则x=3”的逆否命题为:“若x≠3,则x2-4x+3≠0”.
③“x>1”是“|x|>0”的充分不必要条件
④关于x的不等式|x+1|+|x-3|≥m的解集为R,则m≤4.
其中所有正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若任意的a、b∈[-1,1],当a+b≠0时,总有![]() .
.
(1)判断函数f(x)在[-1,1]上的单调性,并证明你的结论;
(2)解不等式:![]() ;
;
(3)若f(x)≤m2-2pm+1对所有的x∈[-1,1]恒成立,其中p∈[-1,1](p是常数),试用常数p表示实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,满足c=1,且cosBsinC+(a﹣sinB)cos(A+B)=0
(1)求C的大小;
(2)求a2+b2的最大值,并求取得最大值时角A,B的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com