
【题目】如图,已知正方体![]() 的棱长为2,则以下四个命题中错误的是
的棱长为2,则以下四个命题中错误的是
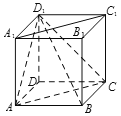
A. 直线![]() 与
与![]() 为异面直线 B.
为异面直线 B. ![]() 平面
平面![]()
C. ![]() D. 三棱锥
D. 三棱锥![]() 的体积为
的体积为![]()
【答案】D
【解析】分析:在A中,由异面直线判定定理得直线A1C1与AD1为异面直线;在B中,由A1C1∥AC,得A1C1∥平面ACD1;在C中,由AC⊥BD,AC⊥DD1,得AC⊥面BDD1,从而BD1⊥AC;在D中,三棱锥D1﹣ADC的体积为![]() .
.
详解:由正方体ABCD﹣A1B1C1D1的棱长为2,知:
在A中,直线A1C1平面A1B1C1D1,BD1平面A1B1C1D1,
D1直线A1C1,由异面直线判定定理得直线A1C1与AD1为异面直线,故A正确;
在B中,∵A1C1∥AC,A1C1平面ACD1,AC平面ACD1,
∴A1C1∥平面ACD1,故B正确;
在C中,∵正方体ABCD﹣A1B1C1D1中,AC⊥BD,AC⊥DD1,
∵BD∩DD1,∴AC⊥面BDD1,∴BD1⊥AC,故C正确;
在D中,三棱锥D1﹣ADC的体积:
![]() =
=![]() =
=![]() ,故D错误.
,故D错误.
故选:D.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】为了解某社区居民有无收看“奥运会开幕式”,某记者分别从某社区60~70岁,40~50岁,20~30岁的三个年龄段中的160人,240人,x人中,采用分层抽样的方法共抽查了30人进行调查,若在60~70岁这个年龄段中抽查了8人,那么x为( ) .
A. 90 B. 120 C. 180 D. 200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若 ![]() =λ
=λ ![]() +μ
+μ ![]() ,则λ+μ的最大值为( )
,则λ+μ的最大值为( )
A.3
B.2 ![]()
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2x,过点(2,0)的直线l交C与A,B两点,圆M是以线段AB为直径的圆.
(Ⅰ)证明:坐标原点O在圆M上;
(Ⅱ)设圆M过点P(4,﹣2),求直线l与圆M的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.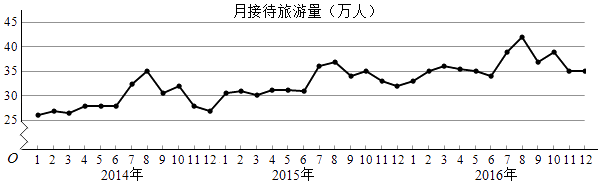
根据该折线图,下列结论错误的是( )
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)求直线![]() 所过定点
所过定点![]() 的坐标;
的坐标;
(2)求直线![]() 被圆
被圆![]() 所截得的弦长最短时
所截得的弦长最短时![]() 的值及最短弦长.
的值及最短弦长.
(3)在(2)的前提下,若![]() 为直线
为直线![]() 上的动点,且圆
上的动点,且圆![]() 上存在两个不同的点到点
上存在两个不同的点到点![]() 的距离为1,求点
的距离为1,求点![]() 的横坐标的取值范围.
的横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设![]() 的顶点分别为
的顶点分别为![]() ,圆
,圆![]() 是
是![]() 的外接圆,直线
的外接圆,直线![]() 的方程是
的方程是![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)证明:直线![]() 与圆
与圆![]() 相交;
相交;
(3)若直线![]() 被圆
被圆![]() 截得的弦长为3,求
截得的弦长为3,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com