

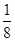 m时,总造价最低,为38882元.
m时,总造价最低,为38882元.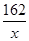 m
m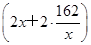 +248×2x+80×162=1296x+
+248×2x+80×162=1296x+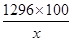 +12960=1296
+12960=1296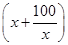 +12960≥1296×2
+12960≥1296×2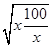 +12960=38880元.当且仅当x=
+12960=38880元.当且仅当x=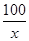 (x>0),即x=10时取等号.∴当长为16.2m,宽为10m时总造价最低,最低总造价为38880元.
(x>0),即x=10时取等号.∴当长为16.2m,宽为10m时总造价最低,最低总造价为38880元.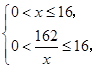 ∴10
∴10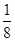 ≤x≤16.设g(x)+x+
≤x≤16.设g(x)+x+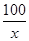
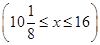 ,由函数性质易知g(x)在
,由函数性质易知g(x)在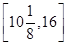 上是增函数,∴当x=10
上是增函数,∴当x=10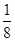 时(此时
时(此时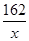 =16),g(x)有最小值,即f(x)有最小值1296×
=16),g(x)有最小值,即f(x)有最小值1296×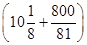 +12960=38882(元).∴当长为16m,宽为10
+12960=38882(元).∴当长为16m,宽为10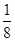 m时,总造价最低,为38882元.
m时,总造价最低,为38882元.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源:不详 题型:单选题
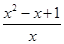 是定义在区间
是定义在区间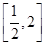 上的“兄弟函数”,那么函数f(x)在区间
上的“兄弟函数”,那么函数f(x)在区间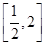 上的最大值为( )
上的最大值为( )A. | B.2 | C.4 | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com