
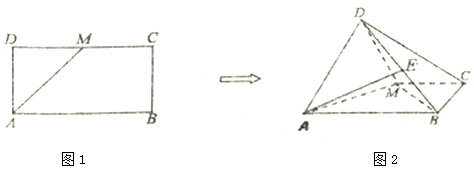
分析 (Ⅰ)取AM的中点N,连接DN.由已知结合面面垂直的性质可得DN⊥平面ABCM.求出DN,然后利用等积法求得三棱锥M-BCD的体积;
(Ⅱ)假设AE⊥BM,结合(Ⅰ)利用反证法证明.
解答 (Ⅰ)解:取AM的中点N,连接DN.
∵AB=2AD,∴DM=AD,又N为AM的中点,
∴DN⊥AM,
∵平面ADM⊥平面ABCM,又平面ADM∩ABCM=AM,DN?平面ADM,
∴DN⊥平面ABCM.
∵AB=2,∴AD=1,AM=$\sqrt{2}$,则$DN=\frac{{\sqrt{2}}}{2}$,
又${S_{△BCM}}=\frac{1}{2}•CM•CB=\frac{1}{2}$,
∴VM-BCD=VD-BCM=$\frac{1}{3}{S}_{△BCM}•DN=\frac{1}{3}×\frac{1}{2}×\frac{\sqrt{2}}{2}=\frac{\sqrt{2}}{12}$;
(Ⅱ)证明:假设AE⊥BM.
由(Ⅰ)可知,DN⊥平面ABCM,∴BM⊥DN.
在长方形ABCD中,AB=2AD,
∴△ADM、△BCM都是等腰直角三角形,∴BM⊥AM.
而DN、AM?平面ADM,DN∩AM=N,
∴BM⊥平面ADM.
而AD?平面ADM,
∴BM⊥AD.
由假设AE⊥BM,AD、AE?平面ABD,AD∩AE=A,
∴BM⊥平面ABD,
而AB?平面ABD,∴BM⊥AB,
这与已知ABCD是长方形矛盾,
故AE不可能与BM垂直.
点评 本题考查直线与平面垂直的性质,考查空间想象能力和思维能力,训练了利用等积法求多面体的体积,训练了一种证明几何问题的方法-反证法,属中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|3≤x<7}, | B. | {x|2<x<10} | C. | {x|x≤2或x≥10} | D. | {x|x<3或x≥7} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∪B=R | B. | A∩B≠∅ | C. | A∪B=∅ | D. | A∩B=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
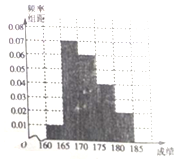 某学校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示:
某学校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 投资结果 | 获利40% | 不赔不赚 | 亏损20% |
| 概 率 | $\frac{1}{3}$ | $\frac{1}{2}$ | $\frac{1}{6}$ |
| 投资结果 | 获利20% | 不赔不赚 | 亏损10% |
| 概 率 | p | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com