
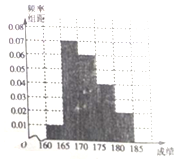
 ijѧУ�������������Գɼ��������ȡ100��ѧ���ı��Գɼ������ɼ����飺��1��[160��165������2��[165��170������3��[170��175������4��[175��180������5��[180��185]���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
ijѧУ�������������Գɼ��������ȡ100��ѧ���ı��Գɼ������ɼ����飺��1��[160��165������2��[165��170������3��[170��175������4��[175��180������5��[180��185]���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������ ��1������Ƶ�ʷֲ�ֱ��ͼ�����Ӧ��Ƶ��ֵ���ɣ�
��2�������3��4��5�鹲��60��ѧ�����������÷ֲ������60��ѧ���г�ȡ6��ѧ�����õ���3��4��5��ֱ��ȡ��������
��3��������6��ѧ���������ȡ2��ѧ�����¼����ܼ��ٵ������¼�A����4��������һ��ѧ������������Ϊ�¼�B���¼�A�����Ļ����¼���Ϊ${C}_{2}^{2}$+${C}_{2}^{1}$${C}_{4}^{1}$���¼�B�����Ļ����¼���Ϊ${C}_{6}^{2}$���ɴ��������4��������һ��ѧ�����������Եĸ��ʣ�
��� �⣺��1���������֪����3���Ƶ��Ϊ0.06��5=0.3��
��4���Ƶ��Ϊ0.04��5=0.2��
��4���Ƶ��Ϊ0.02��5=0.1��
��2����3�������Ϊ0.3��100=30��
��4�������Ϊ0.2��100=20��
��5�������Ϊ0.1��100=10��
��Ϊ��3��4��5�鹲��60��ѧ����
�������÷ֲ������60��ѧ���г�ȡ6��ѧ����
ÿ���ȡ�������ֱ�Ϊ��3�飺$\frac{30}{60}$��6=3��
��4�飺$\frac{20}{60}$��6=2����5�飺$\frac{10}{60}$��6=1��
���Ե�3��4��5��ֱ��ȡ3�ˡ�2�ˡ�1�ˣ�
��3��������6��ѧ���������ȡ2��ѧ�����¼����ܼ��ٵ������¼�A��
��4��������һ��ѧ������������Ϊ�¼�B��
�¼�A�����Ļ����¼���Ϊ${C}_{2}^{2}$+${C}_{2}^{1}$${C}_{4}^{1}$��
�¼�B�����Ļ����¼���Ϊ${C}_{6}^{2}$��
���Ե�4��������һ��ѧ�����������Եĸ���Ϊ
p=$\frac{{C}_{2}^{2}{{+C}_{2}^{1}C}_{4}^{1}}{{C}_{6}^{2}}$=$\frac{3}{5}$��
���� ���⿼��Ƶ�ʷֲ�ֱ��ͼ��Ӧ�ã��ǻ����⣮����ʱҪ�������⣬��ϸ���


 �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д� ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{4}$ | B�� | $\frac{5}{3}$ | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | p��q | B�� | p��q | C�� | �Vp��q | D�� | �Vp��q |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|0��x��2} | B�� | {x|-1��x��3} | C�� | {x|-1��x��0} | D�� | {x|2��x��3} |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com