
分析 (Ⅰ)求导,f′(x)=ex-$\frac{e}{x}$,f(1)=0,f′(1)=0,y=f(x)在(1,f(1))处切线方程为y=0;
(Ⅱ)由题意可知:f′(x)=ex-$\frac{a}{x}$,在($\frac{a}{e}$,1)上是单调递增函数,则?x0∈($\frac{a}{e}$,1)使得${e}^{{x}_{0}}$-$\frac{a}{{x}_{0}}$=0,根据函数的零点判定定理,f(x)有极小值f(x0),由${e}^{{x}_{0}}$-$\frac{a}{{x}_{0}}$=0,构造辅助函数,求导,根据函数的单调性即可求得f(x0)>0,即f(x)在区间$(\frac{a}{e},1)$上有极小值,函数f(x)的极小值大于0.
解答 解:(Ⅰ)由f(x)=ex-alnx-a,x>0,
由a=e,则f(x)=ex-e(lnx-1),求导f′(x)=ex-$\frac{e}{x}$,
由f(1)=0,f′(1)=0,
∴y=f(x)在(1,f(1))处切线方程为y=0,
(Ⅱ)由a∈(0,e),则导f′(x)=ex-$\frac{a}{x}$,在($\frac{a}{e}$,1)上是单调递增函数,
由f′($\frac{a}{e}$)=${e}^{\frac{a}{e}}$-e<0,f′(1)=e-a>0,
则?x0∈($\frac{a}{e}$,1)使得${e}^{{x}_{0}}$-$\frac{a}{{x}_{0}}$=0,
∴?x∈($\frac{a}{e}$,x0),f′(x0)<0,?x∈(x0,1),f′(x0)>0,
故f(x)在($\frac{a}{e}$,x0)上单调递减,在(x0,1)上单调递增,
∴f(x)有极小值f(x0),由${e}^{{x}_{0}}$-$\frac{a}{{x}_{0}}$=0,
则f(x0)=${e}^{{x}_{0}}$-a(lnx0+1)=a($\frac{1}{{x}_{0}}$-lnx0-1),
设g(x)=a($\frac{1}{x}$-lnx-1),x∈($\frac{a}{e}$,1),
g′(x)=a(-$\frac{1}{{x}^{2}}$-$\frac{1}{x}$)=-$\frac{a(1+x)}{{x}^{2}}$,
∴g(x)在($\frac{a}{e}$,1)上单调递减,
∴g(x)>g(1)=0,
即f(x0)>0,
∴函数f(x)的极小值大于0.
点评 本题考查导数的综合应用,导数与函数单调性及极值的关系,函数零点定理,考查转化思想,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|3≤x<7}, | B. | {x|2<x<10} | C. | {x|x≤2或x≥10} | D. | {x|x<3或x≥7} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∪B=R | B. | A∩B≠∅ | C. | A∪B=∅ | D. | A∩B=∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
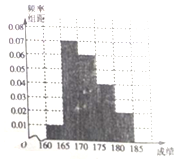 某学校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示:
某学校在自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[160,165),第2组[165,170),第3组[170,175),第4组[175,180),第5组[180,185],得到的频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.
如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com