
分析 先根据数列关系式得到a1+(a2+a3)+(a4+a5)+…+(a2n-2+a2n-1)=1+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{4}}$+…+$\frac{1}{{3}^{2n-2}}$,再根据等比数列的求和公式计算,最后求极限.
解答 解:∵${a_{n+1}}+{a_n}={(\frac{1}{3})^n}$,n∈N,
∴a1+(a2+a3)+(a4+a5)+…+(a2n-2+a2n-1),
=1+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{4}}$+…+$\frac{1}{{3}^{2n-2}}$,
=1+$\frac{\frac{1}{9}(1-\frac{1}{{3}^{2n-2}})}{1-\frac{1}{9}}$,
=1+$\frac{1}{8}$-$\frac{1}{8×{3}^{2n-1}}$,
=$\frac{9}{8}$-$\frac{1}{8×{3}^{2n-1}}$,
∴$\lim_{n→∞}({a_1}+{a_2}+{a_3}+…+{a_{2n-1}})$=$\underset{lim}{n→∞}$($\frac{9}{8}$-$\frac{1}{8×{3}^{2n-1}}$)=$\frac{9}{8}$,
故答案为:$\frac{9}{8}$
点评 本题考查了等比数列的求和公式和极限的定义,考查了学生的运算能力,属于中档题


科目:高中数学 来源: 题型:选择题
| A. | 半径为4的圆的面积 | B. | 半径为4的半圆的面积 | ||
| C. | 半径为4的圆面积的$\frac{1}{4}$ | D. | 半径为16的圆面积的$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 这个算法可以求方程所有的零点 | |
| B. | 这个算法可以求任何方程的零点 | |
| C. | 这个算法能求方程所有的近似零点 | |
| D. | 这个算法并不一定能求方程所有的近似零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2x-3x | B. | f(x)=x3+x2 | C. | f(x)=sinxtanx | D. | $f(x)=lg\frac{1-x}{1+x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
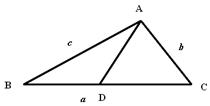 如图,设△ABC的内角A,B,C所对边的长分别是a,b,c,A=$\frac{3π}{4}$,c=6,b=3$\sqrt{2}$,点D在BC边上,且AD=BD,求AD的长.
如图,设△ABC的内角A,B,C所对边的长分别是a,b,c,A=$\frac{3π}{4}$,c=6,b=3$\sqrt{2}$,点D在BC边上,且AD=BD,求AD的长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com