练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．已知函数$y=\frac{{|{{x^2}+x-2}|}}{x-1}$与函数y=kx-2的图象恰有两个交点，则实数k的取值范围是（-1，1）∪（1，5）．

    分析 化简函数的解析式，画出两个函数的图象，判断k的范围即可．

    解答 解：$f（x）=\frac{{|{（x+2）（x-1）}|}}{x-1}=\left\{\begin{array}{l}-x-2，-2≤x＜1\\ x+2，x＜-2或x＞1.\end{array}\right.$
    直线y=kx-2过定点（0，-2），
    由函数图象：
    可知结果为：（-1，1）∪（1，5）．
    给答案为：（-1，1）∪（1，5）．

    点评 本题考查函数与方程的应用，函数的零点个数的判断，考查数形结合思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    7．已知复数z满足（3-i）z=2+i（i为虚数单位），则z的共轭复数是（　　）
    A．$\frac{1}{2}$+$\frac{1}{2}$iB．$\frac{1}{2}$-$\frac{1}{2}i$C．-$\frac{1}{2}$+$\frac{1}{2}$iD．-$\frac{1}{2}$-$\frac{1}{2}$i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

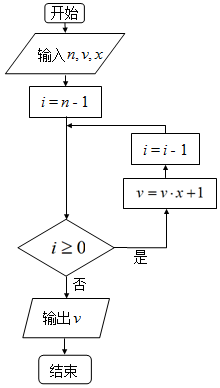    8．我国南宋时期的数学家秦九韶（约1202-1261）在他的著作《数书九章》中提出了多项式求值的秦九韶算法．如图所示的框图给出了利用秦九韶算法求多项式的一个实例．若输入的n=5，v=1，x=2，则程序框图计算的是（　　）
    A．25+24+23+22+2+1B．25+24+23+22+2+5
    C．26+25+24+23+22+2+1D．24+23+22+2+1

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

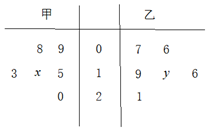    5．如图茎叶图记录了甲，乙两班各六名同学一周的课外阅读时间（单位：小时），已知甲班数据的平均数为13，乙班数据的中位数为17，那么x的位置应填3；y的位置应填8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知椭圆E：mx2+y2=1（m＞0）．
    （Ⅰ）若椭圆E的右焦点坐标为$（\sqrt{3}，0）$，求m的值；
    （Ⅱ）由椭圆E上不同三点构成的三角形称为椭圆的内接三角形．若以B（0，1）为直角顶点的椭圆E的内接等腰直角三角形恰有三个，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=xsinx+cosx．
    （1）当$x∈（\frac{π}{4}，π）$时，求函数f（x）的单调区间；
    （2）若存在$x∈（\frac{π}{4}，\frac{π}{2}）$，使得f（x）＞kx2+cosx成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．在凸四边形ABCD中，BD=2，且$\overrightarrow{AC}•\overrightarrow{BD}=0$，$（\overrightarrow{AB}+\overrightarrow{DC}）•（\overrightarrow{BC}+\overrightarrow{AD}）=5$，则四边形ABCD的面积为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．若数列{an}为等差数列，S99=198，则a48+a49+a50+a51+a52=（　　）
    A．7B．8C．10D．11

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．若圆x2+y2-4x-4y-10=0上至少有三个不同的点到直线l：y=x+b的距离为$2\sqrt{2}$，则b取值范围为[-2，2]．

    查看答案和解析>>

    同步练习册答案