
| 组别 | 一 | 二 | 三 | 四 | 五 |
| 候车时间 | [0,5) | [5,10) | [10,15) | [15,20) | [20,25] |
| 人数 | 2 | 6 | 4 | 2 | l |
分析 (Ⅰ)候车时间少于10分钟的人数所占的比例为$\frac{2+6}{15}$,用60乘以此比例,即得所求.
(Ⅱ)从这6人中选2人作进一步的问卷调查,①用列举法列出上述所有可能情况共有15种,②用列举法求得抽到的两人恰好来自不同组的情况共计8种,由此求得抽到的两人恰好来自不同组的概率
解答 解:(Ⅰ)候车时间少于10分钟的人数所占的比例为$\frac{2+6}{15}$=$\frac{8}{15}$,
故这60名乘客中候车时间少于10分钟的人数为 60×$\frac{8}{15}$=32.
(Ⅱ)设表中第三组的4个人分别为a1、a2、a3、a4、第四组的2个人分别为b1、b2,
从这6人中选2人作进一步的问卷调查,
①用列举法列出上述所有可能情况:
(a1,a2)、(a1,a3)、(a1,a4)、(a1,b1)、(a1,b2)、
(a2,a3)、(a2,a4)、(a2,b1)、(a2,b2)、(a3,a4)、
(a3,b1)、(a3,b2)、(a4,b1)、(a4,b2)、(b1,b2),共计15种.
②抽到的两人恰好来自不同组的情况有
(a1,b1)、(a1,b2)、(a2,b1)、(a2,b2)、
(a3,b1)、(a3,b2)、(a4,b1)、(a4,b2),共计8种,
故抽到的两人恰好来自不同组的概率为$\frac{8}{15}$
点评 本题考查古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,应用列举法来解题是这一部分的最主要思想,属于基础题


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:选择题
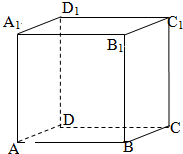 ABCD-A1B1C1D1是单位正方体,黑白两只蚂蚁从点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.白蚂蚁爬行的路线是AA1→A1D1,…,黑蚂蚁爬行的路线是AB→BB1,…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(i∈N*),设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处,则此时黑白蚂蚁的距离是( )
ABCD-A1B1C1D1是单位正方体,黑白两只蚂蚁从点A出发沿棱向前爬行,每爬完一条棱称为“爬完一段”.白蚂蚁爬行的路线是AA1→A1D1,…,黑蚂蚁爬行的路线是AB→BB1,…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(i∈N*),设黑白蚂蚁都爬完2015段后各自停止在正方体的某个顶点处,则此时黑白蚂蚁的距离是( )| A. | $\sqrt{2}$ | B. | 1 | C. | 0 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 喜爱程度 | 非常喜欢 | 一般 | 不喜欢 |
| 人数 | 500 | 200 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,□ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,BM=$\frac{2}{3}$BC,AN=$\frac{1}{4}$AB,
如图所示,□ABCD中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AD}$=$\overrightarrow{b}$,BM=$\frac{2}{3}$BC,AN=$\frac{1}{4}$AB,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$=$\overrightarrow{b}$ | B. | |$\overrightarrow{a}$|=|$\overrightarrow{b}$| | C. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | D. | $\overrightarrow{a}$∥$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个红球与都是黑球 | B. | 至少有一个红球与恰有一个黑球 | ||
| C. | 至少有一个红球与至少有一个黑球 | D. | 恰有一个红球与恰有两个红球 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com