
【题目】已知函数![]() ,
,![]()
(1)当![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)当![]() ,讨论
,讨论![]() 的零点个数;
的零点个数;
【答案】(1)![]() 单调递减区间为:
单调递减区间为:![]() ,
,![]() ;单调递增区间为:
;单调递增区间为:![]() ,
,![]() ;(2)当
;(2)当![]() 时,
时,![]() 在
在![]() 上有2个零点,当
上有2个零点,当![]() 时,
时,![]() 在
在![]() 上无零点.
上无零点.
【解析】
(1)先判断![]() 为偶函数,再利用导数研究
为偶函数,再利用导数研究![]() 上的单调性,根据偶函数的对称性,得到答案.(2)先求出导函数,然后对
上的单调性,根据偶函数的对称性,得到答案.(2)先求出导函数,然后对![]() 按照
按照![]() ,
,![]() ,进行分类讨论,当
,进行分类讨论,当![]() ,得到
,得到![]() 在
在![]() 单调递增,结合
单调递增,结合![]() ,判断出此时无零点,当
,判断出此时无零点,当![]() ,得到
,得到![]() 单调性,结合
单调性,结合![]() ,
,![]() 的值,以及偶函数的性质,得到零点个数.
的值,以及偶函数的性质,得到零点个数.
解:∵![]() ∴
∴![]() 为偶函数,
为偶函数,
只需先研究![]()
![]()
![]()
当![]() ,
,![]() ,当
,当![]() ,
,![]() ,
,
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() ,单调递减
,单调递减
所以根据偶函数图像关于![]() 轴对称,
轴对称,
得![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
.故![]() 单调递减区间为:
单调递减区间为:![]() ,
,![]() ;单调递增区间为:
;单调递增区间为:![]() ,
,![]()
(2)![]()
①![]() 时,
时,![]() 在
在![]() 恒成立
恒成立
∴![]() 在
在![]() 单调递增
单调递增
又![]() ,所以
,所以![]() 在
在![]() 上无零点
上无零点
②![]() 时,
时,![]() ,
,
使得![]() ,即
,即![]() .
.
又![]() 在
在![]() 单调递减,
单调递减,
所以![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() 单调递增,
单调递增,![]() ,
,![]() 单调递减,
单调递减,
又![]() ,
,![]()
(i)![]() ,即
,即![]() 时
时
![]() 在
在![]() 上无零点,
上无零点,
又![]() 为偶函数,所以
为偶函数,所以![]() 在
在![]() 上无零点
上无零点
(ii)![]() ,即
,即![]()
![]() 在
在![]() 上有1个零点,
上有1个零点,
又![]() 为偶函数,所以
为偶函数,所以![]() 在
在![]() 上有2个零点
上有2个零点
综上所述,当![]() 时,
时,![]() 在
在![]() 上有2个零点,当
上有2个零点,当![]() 时,
时,![]() 在
在![]() 上无零点.
上无零点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】端午节(每年农历五月初五),是中国传统节日,有吃粽子的习俗.某超市在端午节这一天,每售出![]() kg粽子获利润
kg粽子获利润![]() 元,未售出的粽子每
元,未售出的粽子每![]() kg亏损
kg亏损![]() 元.根据历史资料,得到销售情况与市场需求量的频率分布表,如下表所示.该超市为今年的端午节预购进了
元.根据历史资料,得到销售情况与市场需求量的频率分布表,如下表所示.该超市为今年的端午节预购进了![]() kg粽子.以
kg粽子.以![]() (单位:kg,
(单位:kg,![]() )表示今年的市场需求量,
)表示今年的市场需求量,![]() (单位:元)表示今年的利润.
(单位:元)表示今年的利润.
市场需求量(kg) |
|
|
|
|
|
频率 | 0.1 | 0.2 | 0.3 | 0.25 | 0.15 |
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)在频率分布表的市场需求量分组中,以各组的区间中间值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中间值的概率(例如:若需求量![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率
的频率![]() ),求
),求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为![]() 的菱形
的菱形![]() 中,
中,![]() .点
.点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,点
上,点![]() 与点
与点![]() ,
,![]() 不重合,
不重合,![]() ,
,![]() .沿
.沿![]() 将
将![]() 翻折到
翻折到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)当![]() 与平面
与平面![]() 所成的角为
所成的角为![]() 时,求平面
时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,已知
中,已知![]() ,
,![]() 为抛物线
为抛物线![]() :
:![]() 上两点,
上两点,![]() 为抛物线焦点.分别过
为抛物线焦点.分别过![]() ,
,![]() 作抛物线的切线交于点
作抛物线的切线交于点![]() .
.
(1)若![]() ,求
,求![]() ;
;
(2)若![]() ,
,![]() 分别交
分别交![]() 轴于
轴于![]() ,
,![]() 两点,试问
两点,试问![]() 的外接圆是否过定点?若是,求出该定点坐标,若不是,请说明理由.
的外接圆是否过定点?若是,求出该定点坐标,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知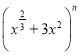 展开式中,各项系数和比它的二项式系数和大992,则下列结论正确的是( )
展开式中,各项系数和比它的二项式系数和大992,则下列结论正确的是( )
A.展开式中的有理项是第2项和第5项B.展开式中没有常数项
C.展开式中二项式系数最大的项是第3项和第4项D.展开式中系数最大的项是第5项
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为4.
,短轴长为4.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作两条直线,分别交椭圆
作两条直线,分别交椭圆![]() 于
于![]() ,
,![]() 两点(异于
两点(异于![]() 点).当直线
点).当直线![]() ,
,![]() 的斜率之和为定值
的斜率之和为定值![]() 时,直线
时,直线![]() 是否恒过定点?若是,求出定点坐标;若不是,请说明理由.
是否恒过定点?若是,求出定点坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线的顶点为A,焦点为F.过F作直线l与抛物线交于点P、Q,直线AP、AQ分别与抛物线的准线交于点M、N.问:直线l满足什么条件时,三直线PN、QM、AF恒交于一点?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.已知随机变量![]() ,若
,若![]() .则
.则![]()
B.已知分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观察值为
的观察值为![]() ,则当
,则当![]() 的值越大时,“
的值越大时,“![]() 与
与![]() 有关”的可信度越小.
有关”的可信度越小.
C.在线性回归模型中,计算其相关指数![]() ,则可以理解为:解析变量对预报变量的贡献率约为
,则可以理解为:解析变量对预报变量的贡献率约为![]()
D.若对于变量![]() 与
与![]() 的
的![]() 组统计数据的线性回归模型中,相关指数
组统计数据的线性回归模型中,相关指数![]() .又知残差平方和为
.又知残差平方和为![]() .那么
.那么![]() .(注意:
.(注意: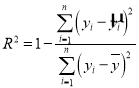 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com