练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设抛物线的顶点为A，焦点为F.过F作直线l与抛物线交于点P、Q，直线AP、AQ分别与抛物线的准线交于点M、N.问：直线l满足什么条件时，三直线PN、QM、AF恒交于一点？

    【答案】见解析

    【解析】

    当直线时，由抛物线的对称性可知，四边形PQMN是矩形，此时，三直线PN、QM、AF互相平行.

    当直线l不与AF垂直时，建立如图的直角坐标系.

    设抛物线的方程为，

    并设、.

    由，得.

    故，.

    因为，所以，，.

    由及分别得，.

    故，

    令y=0，则

    故PN、QM与AF的交点分别为、.

    于是，三直线PN、QM、AF交于一点点S和T重合

    .

    化简得

    将，代入上式得

    即.

    因为，所以，上式成立.

    此时，三直线PN、QM、AF恒交于一点.

    综上所述，当直线l不与AF垂直时，三直线PN、QM、AF交于一点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列说法中，正确的命题是（ ）

    A.已知随机变量服从正态分布，，则

    B.由独立性检验可知，有99%的把握认为物理成绩与数学成绩有关，某人数学成绩优秀，则他有99%的可能物理优秀

    C.以模型去拟合一组数据时，为了求出回归方程，设，将其变换后得到线性方程，则c，k的值分别是和0.3

    D.在回归分析模型中，残差平方和越大，说明模型的拟合效果越差

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （1）当时，求的单调区间；

    （2）当，讨论的零点个数；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为推动乒乓球运动的发展，某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名，其中种子选手2名；乙协会的运动员5名，其中种子选手3名.从这8名运动员中随机选择4人参加比赛.

    （1）设A为事件“选出的4人中恰有2名种子选手，且这2名种子选手来自同一个协会”，求事件发生的概率；

    （2）设为选出的4人中种子选手的人数，求随机变量的分布列.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在班级活动中，4名男生和3名女生站成一排表演节目：（写出必要的数学式，结果用数字作答）

    （1）女生甲不能站在左端，女生乙不能站在右端，有多少种不同的排法？

    （2）甲乙丙三人按高低从左到右有多少种不同的排法？（甲乙丙三位同学身高互不相等）

    （3）现在有7个座位连成一排，仅安排4个男生就坐，怡好有两个空座位相邻的不同坐法共有多少种？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，且经过点.

    （1）求椭圆的标准方程；

    （2）过点的直线交椭圆于两点，是轴上的点，若是以为斜边的等腰直角三角形， 求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图,是正方形ABCD的外接圆,点P在劣弧AB上(P不与A、B重合),DP分别交AO、AB于点Q、T, 在点P处的切线交DA的延长线于点E,劣弧BC的中点为F.

    (1)问:何时F、T、E三点共线?请说明理由.

    (2)求比值的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

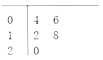
    【题目】某县共有90间农村淘宝服务站，随机抽取5间，统计元旦期间的网购金额（单位：万元）的茎叶图如图所示，其中茎为十位数，叶为个位数．若网购金额（单位：万元）不小于18的服务站定义为优秀服务站，其余为非优秀服务站．从随机抽取的5间服务站中再任取2间作网购商品的调查，则恰有1间是优秀服务站的概率为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】正整数数列满足：，．试求通项公式．

    查看答案和解析>>

    同步练习册答案