
分析 由已知直线的方程求出其倾斜角的正切值,利用二倍角的正确求得所求直线的斜率,代入直线方程的点斜式得答案.
解答 解:设直线y=$\sqrt{3}$x+3的倾斜角为α,则tanα=$\sqrt{3}$.
∴tan2α=$\frac{2tanα}{1-ta{n}^{2}α}=\frac{2\sqrt{3}}{1-(\sqrt{3})^{2}}=-\sqrt{3}$.
即所求直线的斜率为$-\sqrt{3}$.
由直线方程的点斜式得所求直线方程为y-2=$-\sqrt{3}(x-3)$.
整理得:$\sqrt{3}x+y-2-3\sqrt{3}=0$.
点评 本题考查直线的倾斜角,考查了直线的斜率,训练了倍角公式的应用,是基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
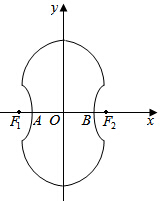 如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶点A、B是该圆与x轴的交点,双曲线与半圆相交于与x轴平行的直径的两端点.
如图所示的“8”字形曲线是由两个关于x轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是x2+y2-4y-4=0,双曲线的左、右顶点A、B是该圆与x轴的交点,双曲线与半圆相交于与x轴平行的直径的两端点.查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(理)试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
如图,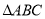 的外接圆为
的外接圆为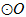 ,延长
,延长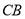 至
至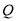 ,再延长
,再延长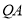 至
至 ,使得
,使得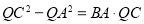 .
.
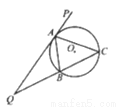
(1)求证: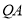 为
为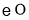 的切线;
的切线;
(2)若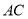 恰好为
恰好为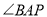 的平分线,
的平分线,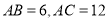 ,求
,求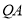 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com