
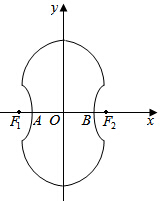 ��ͼ��ʾ�ġ�8����������������������x��ԳƵİ�Բ��һ��˫���ߵ�һ������ɵ�ͼ�Σ������ϰ��Բ����Բ������x2+y2-4y-4=0��˫���ߵ����Ҷ���A��B�Ǹ�Բ��x��Ľ��㣬˫�������Բ�ཻ����x��ƽ�е�ֱ�������˵㣮
��ͼ��ʾ�ġ�8����������������������x��ԳƵİ�Բ��һ��˫���ߵ�һ������ɵ�ͼ�Σ������ϰ��Բ����Բ������x2+y2-4y-4=0��˫���ߵ����Ҷ���A��B�Ǹ�Բ��x��Ľ��㣬˫�������Բ�ཻ����x��ƽ�е�ֱ�������˵㣮���� ��1�������Բ��Բ�ĺͰ뾶�����Բ��x��Ľ��㣬����a=2����y=2����ý��㣬����˫���߷��̣����b�������õ�˫���ߵķ��̣�
��2������������꣬��F1PF2��ֱ�ǣ�����P��x��y��������x2+y2=8����������Բ�ķ��̼�˫���߷��̣���ý��㣬ע����飬���ɵõ������P�����꣮
��3���������ۣ����|MN|�����ɵó����ۣ�
��� �⣺��1���ϰ��Բ����Բ������x2+y2-4y-4=0����Բ��Ϊ��0��2�����뾶Ϊ2$\sqrt{2}$��
���°��Բ����Բ��Բ��Ϊ��0��-2�����뾶Ϊ2$\sqrt{2}$��
˫���ߵ����Ҷ���A��B�Ǹ�Բ��x��Ľ��㣬��Ϊ��-2��0������2��0������a=2��
����˫�������Բ�ཻ����x��ƽ�е�ֱ�������˵㣬����y=2����ã�x=��2$\sqrt{2}$��
���н���Ϊ����2$\sqrt{2}$��2����
��˫���ߵķ���Ϊ$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1��a��0��b��0����
��$\frac{8}{{a}^{2}}$-$\frac{4}{{b}^{2}}$=1����a=2����ã�b=2��
��˫���ߵķ���Ϊ$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}$=1��
��2��˫���ߵ����ҽ���ΪF1��-2$\sqrt{2}$��0����F2��2$\sqrt{2}$��0����
����F1PF2��ֱ�ǣ�����P��x��y��������x2+y2=8��
��$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=8}\\{{x}^{2}-{y}^{2}=4}\end{array}\right.$��ã�x2=6��y2=2��
��$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=8}\\{{x}^{2}+��y��2��^{2}=8}\end{array}\right.$��ã�y=��1�����������⣬��ȥ��
���ڡ�8�����������������P������Ϊ��$��\sqrt{6}��\sqrt{2}$������$��\sqrt{6}��-\sqrt{2}$����
��3����M��N�ĺ�����ֱ�ΪxM��xN��
��ֱ��l��б�ʲ�����ʱ��|MN|=8��
��ֱ��l��б�ʴ���ʱ���跽��Ϊy=k��x+2����
����x2+y2-4y-4=0���ɵã�k2+1��x2+��4k2-4k��x+4k2-8k-4=0��
��-2xM=$\frac{4{k}^{2}-8k-4}{{k}^{2}+1}$��
��xM=$\frac{-2{k}^{2}+4k+2}{{k}^{2}+1}$��
ͬ��xN=$\frac{-2{k}^{2}-4k+2}{{k}^{2}+1}$��
��|MN|=$\sqrt{{k}^{2}+1}$|xM-xN|=$\frac{|8k|}{\sqrt{{k}^{2}+1}}$��8��
��|MN|�����Ϊ8��
���� ���⿼��˫���ߵķ��̵�������Բ��Բ��˫���ߵ�λ�ù�ϵ���������������������е��⣮


 Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017������������и��������ܿ�����ѧ���ģ��Ծ��������棩 ���ͣ������
��ͼ��ʾ�Ķ������У���֪����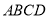 ��ֱ������
��ֱ������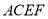 ���ڵ�ƽ�滥�ഹֱ������
���ڵ�ƽ�滥�ഹֱ������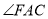 Ϊֱ�ǣ�
Ϊֱ�ǣ�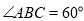 ��
��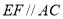 ��
��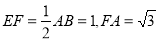 ��
��
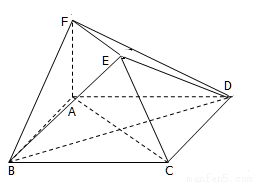
��1����֤��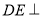 ƽ��
ƽ��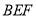 ��
��
��2���������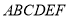 �������
�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2015 | B�� | 2016 | C�� | 2017 | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 4 | C�� | 8 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������������и��������ܿ�����ѧ���ģ��Ծ��������棩 ���ͣ�ѡ����
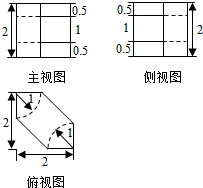
������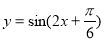 ��ͼ������ƽ��
��ͼ������ƽ��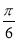 ����λ���������겻�䣬�������Ϊԭ����2����������ͼ��ĺ�������ʽ�ǣ� ��
����λ���������겻�䣬�������Ϊԭ����2����������ͼ��ĺ�������ʽ�ǣ� ��
A��y=sin4x B��y=sinx
C��y=sin��4x��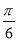 �� D��y=sin��x��
�� D��y=sin��x��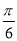 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017������������и��������ܿ�����ѧ�������Ծ��������棩 ���ͣ������
��֪����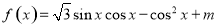
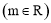 ��ͼ�����
��ͼ�����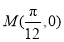 ��
��
������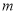 ��ֵ��
��ֵ��
�����ڡ�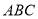 �У���
���� ����
����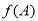 ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 7-$\frac{��}{4}$ | B�� | 7-$\frac{��}{2}$ | C�� | 6-$\frac{��}{2}$ | D�� | 6-�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com