
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | 0 |
分析 利用等差数列的前n项和公式、极限的运算性质即可得出.
解答 解:在等差数列{an}中,∵a1=3,公差d≠0,
∴a1+a3+…+a2n-1=3n+$\frac{n(n-1)}{2}•2d$=dn2+n(3-d),
a2+a4+…+a2n=n(3+d)+$\frac{n(n-1)}{2}•2d$=dn2+3n.
∴$\underset{lim}{n→∞}$$\frac{{a}_{1}+{a}_{3}+…+{a}_{2n-1}}{{a}_{2}+{a}_{4}+…+{a}_{2n}}$=$\underset{lim}{n→∞}\frac{d{n}^{2}+n(3-d)}{d{n}^{2}+3n}$=$\underset{lim}{n→∞}$$\frac{d+\frac{3-d}{n}}{d+\frac{3}{n}}$=$\frac{d}{d}$=1,
故选:C.
点评 本题考查了等差数列的前n项和公式、极限的运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 无数个 |
查看答案和解析>>
科目:高中数学 来源:2017届湖北襄阳四中高三七月周考三数学(文)试卷(解析版) 题型:选择题
将函数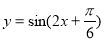 的图象向右平移
的图象向右平移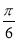 个单位,再纵坐标不变,横坐标变为原来的2倍,所得新图象的函数解析式是( )
个单位,再纵坐标不变,横坐标变为原来的2倍,所得新图象的函数解析式是( )
A.y=sin4x B.y=sinx
C.y=sin(4x﹣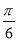 ) D.y=sin(x﹣
) D.y=sin(x﹣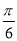 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com