练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设椭圆的右焦点为，过的直线与交于两点，点的坐标为.

    （1）当与轴垂直时，求直线的方程；

    （2）设为坐标原点，证明：.

    【答案】(1) AM的方程为或.

    (2)证明见解析.

    【解析】分析：(1)首先根据与轴垂直，且过点，求得直线l的方程为x=1，代入椭圆方程求得点A的坐标为或，利用两点式求得直线的方程；

    (2)分直线l与x轴重合、l与x轴垂直、l与x轴不重合也不垂直三种情况证明，特殊情况比较简单，也比较直观，对于一般情况将角相等通过直线的斜率的关系来体现，从而证得结果.

    详解：（1）由已知得，l的方程为x=1.

    由已知可得，点A的坐标为或.

    所以AM的方程为或.

    （2）当l与x轴重合时，.

    当l与x轴垂直时，OM为AB的垂直平分线，所以.

    当l与x轴不重合也不垂直时，设l的方程为，，

    则，直线MA，MB的斜率之和为.

    由得

    .

    将代入得

    .

    所以，.

    则.

    从而，故MA，MB的倾斜角互补，所以.

    综上，.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知长方体ABCD-A1B1C1D1中，底面ABCD为正方形，AB=4，AA1=2，点E1在棱C1D1上，且D1E1=3。

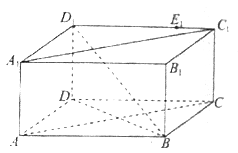
    （I）在棱CD上确定一点E，使得直线EE1∥平面D1DB，并写出证明过程；

    （II）求证：平面A1ACC1⊥平面D1DB；

    （III）若动点F在正方形ABCD内，且AF=2，请说明点F的轨迹，试求E1F长度的最小值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数f(x)定义在区间(0，＋∞)上，且f(1)＝0，导函数f′(x)＝，函数g(x)＝f(x)＋f′(x)．

    (1)求函数g(x)的最小值；

    (2)是否存在x0＞0，使得不等式|g(x)－g(x0)|＜对任意x＞0恒成立？若存在，请求出x0的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C所对边分别是a，b，c，若sin（A﹣B）= sinAcosB﹣ sinBcosA．
    （1）求证：A=B；
    （2）若A= ，a= ，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列{an}的前n项和Sn满足Sn＝，且a1，a2＋1，a3成等差数列．

    （1）求数列{an}的通项公式；

    （2）记数列的前n项和为Tn，求证： Tn＜1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】传承传统文化再掀热潮，央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级，随机从中抽取了100名选手进行调查，下面是根据调查结果绘制的选手等级人数的条形图.

    （1）若将一般等级和良好等级合称为合格等级，根据已知条件完成下面的列联表，据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关？

    优秀

    合格

    合计

    大学组

    中学组

    合计

    注：，其中.

    0.10

    0.05

    0.005

    2.706

    3.841

    7.879

    （2）若参赛选手共6万人，用频率估计概率，试估计其中优秀等级的选手人数.

    （3）在优秀等级的选手中取6名，依次编号为1，2，3，4，5，6.在良好等级的选手中取6名，依次编号为1，2，3，4，5，6，在选出的6名优秀等级的选手中任取一名，记其编号为，在选出的6名良好等级的选手中任取一名，记其编号为，求使得方程组有唯一一组实数解的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点在抛物线上，则当点到点的距离与点到抛物线焦点距离之和取得最小值时，点的坐标为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知不等式组表示的平面区域为，若函数的图象上存在区域内的点，则实数的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ax（a＞0，a≠1）的反函数的图象经过点（ ， ）．若函数g（x）的定义域为R，当x∈[﹣2，2]时，有g（x）=f（x），且函数g（x+2）为偶函数，则下列结论正确的是（ ）
    A.g（π）＜g（3）＜g（ ）
    B.g（π）＜g（ ）＜g（3）??
    C.g（ ）＜g（3）＜g（π）
    D.g（ ）＜g（π）＜g（3）

    查看答案和解析>>

    同步练习册答案